ajohnson1.github.io

Bobs-only extents of Stedman Triples

Click here for table of contents.

Introduction

Back in 1995 the question of whether it was possible to get an extent of Stedman Triples using only common bobs was settled with Colin Wyld’s peals (CompLib 21261 CompLib 37681) and the Johnson/Saddleton peal (CompLib 10423). These peals were one-part compositions with many bobs, and are hard to conduct.

Since then there have been further compositions starting with my 4 irregular 10-part peals from June 1995 with 438 bobs (CompLib 28944 CompLib 28946) and 441 bobs (CompLib 28945 CompLib 28947) which have been rung over 200 times. A further development in 2012 was another 148 10-part peals with between 438 bobs (CompLib 31021) and 456 bobs CompLib 37714), including several exact two-part peals, some with at most 5 bobs in a row. More recently were my exact three-part peals of 2017 (CompLib 36006).

Since then I have come up with many more peals, though they are likely to be too hard to call for most conductors.

There are 840 places (at any six-end) where a bob could be called in an extent of Stedman Triples, which would give $2^{840} = 7.3×10^{253}$ possibilities. This is so huge that a direct search is impossible. Another approach is to cover all the rows with multiple shorter touches, each with a different starting row and returning to its start point (round blocks). You cannot cover all the rows with plain courses (the maximum is 40 of the required 60, but the remaining rows are unlinkable). You can cover all the rows with 84 B-blocks, 60 change round blocks of 10 bobs in a row. The problem then is to link the round blocks together into one big block. Omitting a bob from three B-blocks affecting the same 3 bells behind while the front 4 bells are in the same position can link them into one. That process would at best reduce the number of round blocks down from 84 in twos to give two unlinkable round blocks.

This is an example of the Q-set parity law. With Grandsire Triples using only common bobs there is only one lead head which brings up a row which leads to the proof of the impossibility of a extent of Grandsire Triples using just common bobs. Stedman Triples is made up of sixes, and with bobs and plains any row could appear in a six defined by one of six possible six-ends, three quick or three slow, which breaks the Q-set parity law restriction, similar to how in Cambridge Surprise Minor a row can appear either of two leads, the forward or backwards version, thus allowing a bobs-only 720.

B-blocks have a pair of bells dodging behind and two B-blocks can cover all the rows with a pair of bells dodging a particular way round. For each pair there are six possible complementary pairs of B-blocks, as illustrated by the six-ends below. The QS is my convention for a quick six-end (to be followed by a slow six) and SQ for a slow six-end.

2314567QS
3215467QS

3124567QS
1325467QS

1234567QS
2135467QS

2314567SQ
2134567SQ

3124567SQ
3215467SQ

1234567SQ
1325467SQ

Magic Block Peals

The magic blocks used in the Wyld and Johnson/Saddleton peals have the same rows as 10 B-blocks but in five round blocks, breaking the parity barrier. This is my compact form of showing them, where - means a bob and P means a plain after the six-end, and the *1(1) means the block is rung once, and there is one version of it in the peal (useful for multi-part peals).

2314567QS---------P------P--P*1(1)
2743516QS---------P------P--P*1(1)
2176534QS---------P------P--P*1(1)
2461573QS---------P------P--P*1(1)
2637541QS---------P------P--P*1(1)

Notice how they are a five-part set, with bells 2 and 5 fixed and 3,7,6,1,4 rotating.

There are then 10 B-blocks which are the complementary pairs of those first 10 blocks, and 64 remaining B-blocks, arranged in 32 complementary pairs. There are therefore $6^{32}=7.96×10^{18}$ choices for those pairs, and some choices give enough Q-sets to link everything together. This gives 79 round blocks with 825 bobs, which perhaps could be reduced to one block using 39 Q-sets of 3 omits.

The sixes can be rearranged into 79 complete B-blocks by chopping them up and joining them together without changing the type of the six. There are 64 B-blocks in complementary pairs, 10 B-blocks which partner the magic blocks, and 5 B-blocks which can be obtained from the magic blocks. The other sixes for the other 5 B-blocks cannot by obtained as they are disrupted by the sixes between the P--P sequences of calls.

There have been further minor developments in magic block peals. Colin Wyld found that he needed an extra Q-set of omits to link the blocks together, so the peal took $840-5×3-3×(79-1)/2-3=705$ bobs. With a suitable choice of B-blocks the extra Q-set of omits is not needed and a peal of 708 bobs is possible, for example by bobbing some Q-sets of the first Johnson/Saddleton peal to give CompLib 37705. By bobbing one Q-set of Wyld’s No. 1 then that can also be increased to 708 bobs (CompLib 92949).

With more care then the omits can be all isolated, as shown by CompLib 46033 (rung on 14 March 2019) and CompLib 46069 where there are just 8 omits after quick sixes (5 essential for the magic blocks plus 1 Q-set) and 124 after slow sixes. From my searches I do not think it is possible to reduce this to the 5 essential omits after quick sixes, thus answering Alan Burbidge’s question in ‘Stedman Triples and Similar Fascinations’. These peals can be reversed if required, putting most of the omits after the quick sixes and a few after the slow sixes.

The first bobs-only peal to be rung had 579 bobs. Shortly afterwards, Philip Saddleton reported that he had reduced that to 576 bobs, but did not publish it. I I have now composed a magic block peal with 576 bobs, CompLib 59746, which I believe to be the minimum on the plan.

It is not possible to get a peal using the magic blocks without at least one run of 9 bobs, for example CompLib 91621.

In classifying bobs-only peals it is useful to have some statistics which do not change with the choice of Q-sets plained or bobbed or the choice of pairs of complementary B-blocks.

• Number of round blocks when all Q-sets bobbed.
• Number of bobs when all Q-sets bobbed.
• Number of whole B-blocks when all Q-sets bobbed.
• Number of whole paired B-blocks when all Q-sets bobbed.
• Number of complete B-blocks (take all the sixes, and without changing their type can they be chopped up and reassembled into whole B-blocks).
• Number of paired sixes

In this article, the signature of the peal is obtained by bobbing all Q-sets, then looking at the round blocks. Some might be B-blocks, but others would contain blocks with some plains. The magic blocks have a signature of 10:5+15, which means that the contents of 10 B-blocks are rearranged and linked into 5 round blocks using 15 plains, giving $84-10+5=79$ round blocks including the untouched B-blocks.

When comparing peals other statistics can determine their merit:

• Number of bobs (normally minimised, sometimes maximised)
• Minimise the longest run of bobs
• Minimise the number of runs of an odd number of bobs, so that bells normally alternate going in quick and slow
• Longest run of plain leads, prefer runs ending at a slow six so that the peal can finish in the plain course
• Multiple parts
• Repeated sections
• Number of different courses

Other 79 complete B-block peals

79 round blocks

Recently I discovered some more peals, which although looking similar to magic block peals are in fact different. Some are based on these 3 sets of blocks, giving 4 sets of blocks with 79 complete B-blocks.

Signature: 10:5+15

2314567QS---------P------P--P*1(1)
2471536QS---------P------P--P*1(1)
2736514QS---------P------P--P*1(1)
2167543QS---------P------P--P*1(1)
2643571QS---------P------P--P*1(1)

This looks similar to the magic blocks, but is different, and generates different peals. There is a peal with only 5 plains (omits) after a quick six, CompLib 92794, though with 2 double omits. To avoid double omits however requires at least 18 plains after a quick six. There are peals from 576 bobs (CompLib 92793) to 708 bobs.

These blocks are clearly different as two of the blocks have 9,2,6 bobs in a run rather than 9,6,2.

Signature: 10:5+15

2314567QS---------P------P--P*1(1)
2471536QS---------P------P--P*1(1)
2736514QS---------P------P--P*1(1)
5246317QS--------P--P------P-*1(1)
5217634QS--------P--P------P-*1(1)

There is a peal, CompLib 91638 which has only 7 omits after a quick six, the minimum using these blocks, and isolated omits. A similar peal with 7 omits after a slow six is CompLib 84678 There is also another peal, CompLib 90948 with a maximum of 6 bobs in a run, no 5-bob sets, and only 3 3-bob sets and 36 single bobs, so most of the time the alternation between quick and slow work is maintained.

Signature: 10:5+15

2314567QS---------P------P--P*1(1)
2743516QS---------P------P--P*1(1)
2176534QS---------P------P--P*1(1)
5241637QS--------P--P------P-*1(1)
5236714QS--------P--P------P-*1(1)

This gives another peal, CompLib 92964 with a maximum of 6 bobs in a run, two 5-bob sets, and two 3-bob sets and 37 single bobs. A 579 bob peal is CompLib 84857. CompLib 90545 and CompLib 90546 have only 7 omits after a quick six.

78 complete B-block peals

There are some more peals based on combining all the rows of several B-blocks into larger round blocks. If all the sixes were separated then for these peals it would be possible to arrange them into 78 whole B-blocks with some sixes left over, so in the peal all the pieces of all 78 B-blocks are present and complete. This is for the convenience of classifying the peals as the choice of which pair of B-blocks with the same bells behind does not affect this statistic, neither does adding or removing 3 bobs in a Q-set [where the same 3 bells are affected by the call and the other bells are in the same position at each call]. Here are the 4 sets of blocks.

73 round blocks

Here is the first block.

Signature: 12:1+21

2314567QS---------P--------P-P--------P---------P-P--------PP-------P---------PP-------PP---------PPP--------PP------P---------PP*1(1)

Rotated version of that block: CompLib 90582 Links the contents of 12 whole B-blocks into 1 big block using 21 plains, giving $84-12+1=73$ round blocks including the untouched B-blocks. This leaves 12 more B-blocks as the pairs of those, and 60 paired B-blocks, where each pair can be chosen from one of six, making assembly of the peal quite easy. There are then 73 round blocks to link. By choosing the B-block pairs carefully extra Q-sets can be found which can be plained to reduce the total number of bobs.

• CompLib 90595 576 bobs
• CompLib 85949 576 bobs

There are 73 round blocks formed using 21 plains, so there is the chance of finding $72/2=36$ Q-sets to link them into one block, the peal, which would add another $36×3=108$ plains, so 129 plains and hence 711 bobs, but I have not found a peal using this block with that many bobs.

75 round blocks

Signature: 12:3+21

2314567QS---------P------PP---------PPP------P--P--------P--------P---------PP---------PP*1(1)
2341576QS---------P------P--P*1(1)
2761534QS--------P-------P-PP*1(1)

This takes the contents of 12 whole B-blocks and puts them into 3 round blocks using 21 plains. There are then 12 B-blocks which are pairs of those original blocks before they were reconstituted, and 60 paired remaining B-blocks.

• CompLib 93211 579 bobs

An upper limit of bobs in a peal on this plan is as follows: 21 plains, 75 blocks, so a possible maximum of $840-21-3×(84-12+3-1)/2=708$ bobs.

77 round blocks (a)

Signature: 11:4+18

2314567QS---------P--------P---------PP---------P-P------PP*1(1)
3671245QS---------P------P--P*1(1)
3517246QS--------P-------P-PP*1(1)
2314675QS--------P--P------P-*1(1)

Upper limit of possible bobs: $840-18-3×(84-11+4-1)/2=708$ bobs.

• CompLib 93112 555 bobs
• CompLib 85001 552 bobs (blocks reversed)
• CompLib 88208 549 bobs

Instead of minimising the number of bobs, we can choose to reduce the number of sets of odd numbers of bobs in a run. This helps maintain the alternation of quick and slow work for the bells. Doing that gives the following peal, where the only runs of an odd number of bobs are single bobs, and there are only 18 of them. The 4-bob and 6-bob sets come at the start of the slow for some bell, whereas the 98 of the runs of 2 bobs are in quick, 23 are in slow. The treble does not have any odd bobs behind, just 0,2 or 6 bobs.

• CompLib 84174
  • 594 bobs
  • 18 isolated bobs
  • 121 runs of 2 bobs
  • 7 runs of 4 bobs
  • 51 runs of 6 bobs

I think this peal would not feel like a Thurstans twin-bob peal as there are so many more bobs, but might be slightly easier on the band than other bobs-only peals.

77 round blocks (b)

Signature: 11:4+18

2314567QS---------P-------P---------P-P------PP---------P-P*1(1)
2736514QS---------P------P--P*1(1)
2174563QS--------P-------P-PP*1(1)
5263417QS--------P--P------P-*1(1)

• CompLib 82690 582 bobs
• CompLib 93059 546 bobs This peal has 30 fewer bobs than any magic block peal.
• CompLib 110519 543 bobs This peal has 33 fewer bobs than any magic block peal.

77 complete B-block peals

I have found 8 different ways of rearranging the contents of a whole number of B-blocks to give an odd number of round blocks, subject to the 77 complete B-block restriction.

73 round blocks (a)

Signature: 13:2+21

2314567QS---------P--------P---------P-P---------P--------P---------PP---------P--------P--------P---------PP*1(1)
2173465QS-------PP----PP--------PP--PP-*1(1)

73 round blocks (b)

Signature: 13:2+21

2314567QS---------P--------P---------P-P---------P--------P---------PP---------P--------P--------P---------PP*1(1)
3517246QS--------PP------PP--------PPPP*1(1)

Both have the signature of linking 13 B-blocks into two blocks using 21 plains, so giving 73 round blocks in total. However, I have not found a peal using either of these sets of blocks.

75 round blocks (a)

Signature: 13:4+21

2314567QS---------P--------P---------P-------P--P--------P---------PP*1(1)
2461573QS---------P------PPP--------PPP*1(1)
2416537QS---------P------P--P*1(1)
2743516QS---------P------P--P*1(1)

Signature of 13 B-blocks into four blocks using 21 plains, giving 75 round blocks in total.

• CompLib 85387 579 bobs
• CompLib 93113 576 bobs

Signature: 13:4+21

2314567QS---------P--------P---------P-------P--P--------P---------PP*1(1)
5274631QS--------PPP--------PPP------P-*1(1)
2617534QS---------P------P--P*1(1)
5271364QS--------P--P------P-*1(1)

Signature of 13 B-blocks into four blocks using 21 plains, giving 75 round blocks in total.

• CompLib 118044 591 bobs

75 round blocks

Signature: 14:5+21

2314567QS---------P--------P---------PP---------P--------P---------PP*1(1)
4721536QS---------P------P--P*1(1)
4361572QS---------P------P--P*1(1)
5416732QS--------P--P------P-*1(1)
5172346QS-------P---P-----PP-*1(1)

No peal

75 round blocks (b)

Signature: 14:5+21

2314567QS---------P-----P---------PP---------P--------P---------P---P*1(1)
2764513QS---------P------P--P*1(1)
5246317QS--------P--P------P-*1(1)
5241763QS--------P--P------P-*1(1)
1465327QS-------PP--------PP-*1(1)

Signature of 14 B-blocks into five blocks using 21 plains, giving 75 round blocks in total.

• CompLib 110131 552 bobs

75 round blocks (c)

Signature: 14:5+21

2314567QS---------P-----P---------PP---------P--------P---------P---P*1(1)
2674531QS---------P------P--P*1(1)
5241637QS--------P--P------P-*1(1)
5247361QS--------P--P------P-*1(1)
3146527QS--------PP--------PP*1(1) 

Signature of 14 B-blocks into five blocks using 21 plains, giving 75 round blocks in total.

• CompLib 110132 582 bobs

75 round blocks

Signature: 14:5+21

2314567QS---------PP---------P--------P---------PP---------P--------P*1(1)
7356124QS---------P------P--P*1(1)
7426153QS---------P------P--P*1(1)
1765423QS--------P--P------P-*1(1)
1652374QS-------P---P-----PP-*1(1) 

No peal

76 complete B-block peals

I have found 24 different ways of rearranging the contents of a whole number of B-blocks to give an odd number of round blocks, where the peal can have 76 complete B-blocks extracted from the sixes.

71 round blocks (a)

Signature: 18:5+33

2314567QS---------P--------P---P--PP--P---------P--P-----PP---------P-P---------P-------P*1(1)
6352741QS---------P--P---------P--PP--P*1(1)
1547362QS--------P--P---PP--------PP-P-*1(1)
4371526QS---------P------P--P*1(1)
3265714QS--------P--P------P-*1(1)

This arranges the contents of 18 B-blocks into 5 round blocks using 33 plains, giving 71 round blocks in total.

• CompLib 84985 597 bobs
• CompLib 85836 567 bobs

71 round blocks (b)

Signature: 14:1+24

2314567QS---------P--------P---------P-PP-------PPP------P-P---------P--------P--------P---------PPP-------P---------P-PP-------P--------P---------PP*1(1)

This arranges the contents of 14 B-blocks into 1 round block using 24 plains, giving 71 round blocks in total. No peal.

2314567QS---------P--------P-P--------P---------PP-------PP---------P-P-------P---------PPP---------P------PP--------PPP--------P---------P-P-------P*1(1)

This arranges the contents of 14 B-blocks into 1 round block using 24 plains, giving 71 round blocks in total. This set of blocks has an upper limit of 711 bobs for a peal, and such a peal can be found. 71 blocks to be linked by 35 Q-sets, adding another 105 plains, so giving 129 plains in total.

• CompLib 93425 564 bobs
• CompLib 93428 711 bobs
• CompLib 93429 711 bobs, only 8 omits after a quick six

This core block can be examined. Note how bells 2 and 3 remain together in the front 5 places.

• CompLib 93430 840 changes 116 bobs

71 round blocks (c)

Signature: 19:6+33

2314567QS---------P--------P---------P-------P---------P-P---------PP*1(1)
5431276QS---------P--P--P---------PP--P*1(1)
4216573QS--------P--P---PP--------PP-P-*1(1)
4612753QS--------P--P--P---------P--PP-*1(1)
4561273QS---------P------P--P*1(1)
4721653QS---------P------P--P*1(1)

No peal

71 round blocks (d)

Signature: 19:6+33

2314567QS---------P--------P---------P-------P---------P-P---------PP*1(1)
7351426QS---------P--P--P---------PP--P*1(1)
7641523QS---------P--P--P---------PP--P*1(1)
4216573QS--------P--P---PP--------PP-P-*1(1)
7415326QS--------P--P------P-*1(1)
7514623QS--------P--P------P-*1(1)

No peal

71 round blocks (e)

Signature: 19:6+33

2314567QS---------P-----P---------PP---------P--------P---------P---P*1(1)
3274561QS---------P--P--P---------PPPP--------PPP*1(1)
2145637QS--------P--P--P---------P--PP-*1(1)
2654137QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
3547261QS--------P--P------P-*1(1)

This arranges the contents of 19 B-blocks into 6 round blocks using 33 plains, giving 71 round blocks in total. It does give a peal.

71 round blocks (f)

Signature: 19:6+33

2314567QS---------P-----P---------PP---------P--------P---------P---P*1(1)
6524713QS---------P--P--P---------PP--P*1(1)
6742513QS--------P--P--P---------P--PP-*1(1)
2145763QS--------P--PPP--------PP----P-*1(1)
3264517QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)

Peal.

71 round blocks (g)

Signature: 19:6+33

2314567QS---------P---P---------PP--P---------P-P---------PP---------P--------P*1(1)
4176235QS--------P--P--P---------P--PP-*1(1)
6273541QS--------P--PPP--------PP----P-*1(1)
6537241QS---------P------P--P*1(1)
5647231QS---------P------P--P*1(1)
6372145QS--------P--P------P-*1(1)

• CompLib 109439 540 bobs

71 round blocks (h)

Signature: 19:6+33

2314567QS---------P---P---------PP--P---------P-P---------PP---------P--------P*1(1)
4517632QS---------P--PPP--------PPP---------PP--P*1(1)
6372145QS--------P--P------P-*1(1)
4176235QS--------P--P------P-*1(1)
1375642QS--------P--P------P-*1(1)
4671532QS--------P--P------P-*1(1)

peal

73 round blocks (a)

Signature: 18:7+33

2314567QS---------P-----P------P--PP--P*1(1)
4312576QS---------P--P---------P--PP--P*1(1)
7356124QS---------P--P---------P--PP--P*1(1)
6357142QS---------P--P---------P--PP--P*1(1)
1324657QS---------P------P--P*1(1)
1754623QS---------P------P--P*1(1)
6142753QS--------P--P------P-*1(1)

peal

73 round blocks (b)

Signature: 18:7+33

2314567QS---------P---P------P--P--P--P*1(1)
2315476QS---------PP---------P--P--P--P*1(1)
3217645QS---------PP---------P--P--P--P*1(1)
3216754QS---------PP---------P--P--P--P*1(1)
6514327QS---------P------P--P*1(1)
6274351QS---------P------P--P*1(1)
3647521QS--------P--P------P-*1(1)

This arranges the contents of 18 B-blocks into 7 round blocks using 33 plains, giving 73 round blocks in total.

• CompLib 93427 594 bobs

75 round blocks (a)

Signature: 14:5+21

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
6254317QS---------P------P--P*1(1)
6714352QS---------P------P--P*1(1)
3645712QS--------P--P------P-*1(1)
2743165QS-------PP--------PP-*1(1)

This arranges the contents of 14 B-blocks into 5 round blocks using 21 plains, giving 75 round blocks in total.

• CompLib 82483 591 bobs Only 13 runs with an odd number of bobs: 1 5-bob set, 2 3-bob sets, 10 1-bob sets. Last third of peal is all in pairs (runs of 2 and 6, with one 4).

75 round blocks (b)

Signature: 14:5+21

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
6514327QS---------P------P--P*1(1)
6274351QS---------P------P--P*1(1)
3647521QS--------P--P------P-*1(1)
1274365QS--------PP--------PP*1(1)

This arranges the contents of 14 B-blocks into 5 round blocks using 21 plains, giving 75 round blocks in total.

• CompLib 92787 558 bobs

75 complete B-block peals

With all the sets of blocks I have given I have tried to avoid duplicates by arranging them in a canonical form. For each block, if it is a round block, choose a rotation to give a start which is a quick six. Choose a rotation with the longest runs of bobs first (lexical comparison, - before P). If the block is multi-part (so two rotations can be the same), choose a start with biggest start when the row is reversed (so 2134567 is before 2136745). When there are multiple blocks, rearrange the order of the blocks so the longest block is first, then if equal do by starting six as above. Now consider renumbering the blocks so that the first block is 2134567QS and sort as above. Also try renumbering so another block of the same length is 2134567QS. Also check for reversals by taking each starting six, finding the six-head, then swap 1 & 2 to keep it in course, and reverse the block, then do all the above. See if it is before the best non-reversed version.

I have not given peals for some of the blocks as I did not want to clutter up CompLib with similar peals, but I can add them if anyone is interested. Here are 14 ways of getting an odd number of blocks.

71 round blocks

Signature: 15:2+27

This rearranges the contents of 15 B-blocks into 2 round blocks, giving 71 round blocks.

2314567QS---------P--------P--------P--------P---------P-P--------PP-------P---------PPPP--------P---------PP---------P--------PP*1(1)
2761534QS--------PP------PP--------PPPP*1(1)

no peal

Signature: 19:6+33

These all rearrange the contents of 19 B-blocks into 6 round blocks, giving 71 round blocks.

2314567QS---------P--------P---------P-------P--P--------P---------PP*1(1)
2657431QS---------P---PP--------PP-P--P*1(1)
4173562QS--------P--P--P---------P--PP-*1(1)
5176432QS--------P--P--P---------P--PP-*1(1)
4537162QS---------P------P--P*1(1)
5467132QS---------P------P--P*1(1)

peal

2314567QS---------P--------P---------P-------P--P--------P---------PP*1(1)
2657431QS---------P---PP--------PP-P--P*1(1)
6217435QS---------P--P--P---------PP--P*1(1)
2574361QS--------P--P--P---------P--PP-*1(1)
6471235QS--------P--P------P-*1(1)
2475631QS--------P--P------P-*1(1)

no peal

2314567QS---------P--------P--P-------P---------P-P---------P-------P*1(1)
6527143QS---------PP---------P--P--P--P*1(1)
5623471QS---------PP---------P--P--P--P*1(1)
6172543QS--------P--PP-P-------P-P---P-*1(1)
6521734QS---------P------P--P*1(1)
3245617QS--------P--P------P-*1(1)

peal

2314567QS---------P--------P--P-------P---------P-P---------P-------P*1(1)
7621534QS---------P--P---------P--PP--P*1(1)
4653271QS---------P--P---------P--PP--P*1(1)
6172543QS--------P--PP-P-------P-P---P-*1(1)
6527143QS---------P------P--P*1(1)
4235671QS--------P--P------P-*1(1)

• CompLib 89469 582 bobs

2314567QS---------P--------P--P-------P---------P-P---------P-------P*1(1)
7621534QS---------P--P---------P--PP--P*1(1)
4653271QS---------P--P---------P--PP--P*1(1)
6172543QS--------P--PP-P-------P-P---P-*1(1)
6527143QS---------P------P--P*1(1)
4235671QS--------P--P------P-*1(1)

peal

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
5634712QS---------P--P--P---------PP--P*1(1)
2354617QS---------PPP--------PP----P--P*1(1)
5743612QS--------P--P--P---------P--PP-*1(1)
3214657QS---------P------P--P*1(1)
3146752QS--------P--P------P-*1(1)

• CompLib 93488 555 bobs

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
7543621QS--------P--PP---------PPP--------PPP--P-*1(1)
2374651QS---------P--P--P---------PP--P*1(1)
3214657QS---------P------P--P*1(1)
3564127QS---------P------P--P*1(1)
2647351QS--------P--P------P-*1(1)

peal

2314567QS---------P---PP---------P--P--P--------P---------PP---------P--------P*1(1)
6745123QS--------P--P--P---------PPP--------PPPP-*1(1)
3214657QS---------P------P--P*1(1)
3564127QS---------P------P--P*1(1)
1624753QS---------P------P--P*1(1)
6154723QS---------P------P--P*1(1)

• CompLib 822309 591 bobs

2314567QS---------P--P---------P------P---------P--P---------P------P*1(1)
6357142QS---------P-----P------P--PP--P*1(1)
7356124QS---------P--P---------P--PP--P*1(1)
4523671QS--------P--PPP--------PP----P-*1(1)
4563217QS--------P--P------P-*1(1)
4517326QS--------P--P------P-*1(1)

no peal

2314567QS---------P--P---------P------P---------P--P---------P------P*1(1)
7356124QS---------P-----P------P--PP--P*1(1)
6357142QS---------P--P---------P--PP--P*1(1)
2543761QS--------P--PPP--------PP----P-*1(1)
2516347QS--------P--P------P-*1(1)
2573416QS--------P--P------P-*1(1)

no peal

2314567QS---------P---P--P---------P--PP--------P---------PP---------P--------P*1(1)
5374126QS---------P--P--P---------PP--P*1(1)
3146527QS--------PPP--------PPP------P-*1(1)
3214657QS---------P------P--P*1(1)
3564127QS---------P------P--P*1(1)
5147326QS--------P--P------P-*1(1)

• CompLib 110803 546 bobs

74 complete B-block peals

I have found 44 sets of blocks of getting an odd number of blocks. so far, where the sixes from each set (and the remaining B-blocks) can be rearranged into 74 complete B-blocks.

67 round blocks, signature: 20:3+33

2314567QS---------P--------P------P---P---------P-----P---------P---P---------P-----P--PP---------P--P-----P---P------P*1(1)
7623541QS--------P-----P---------P---P---------P--PP--------PP-P---------P---P-*1(1)
6571324QS-----P---P-----P---P*1(1)

• CompLib 82349 543 bobs, at most 6 bobs in a run
• CompLib 94456 537 bobs, at most 6 bobs in a run

2314567QS---------P--------P-P--------P---------P-P--------PP-------P---------PP-------PP---------PPP--------PP------P---------PP*1(1)
2541367QS--------P-------P---------P-P---------P-------P---------P-P-*1(1)
2456317QS-------P-P-------P-P*1(1)

This set of blocks includes the 12:1+21 block block from 78 complete B-blocks, so the other two blocks link 8 B-blocks into 2 blocks.

• CompLib 85818 570 bobs, 8 plains in a run
• CompLib 82340 543 bobs
• CompLib 85271 531 bobs
• CompLib 82341 531 bobs

2314567QS---------P--------P-P--------P---------P-P--------PP-------P---------PP-------PP---------PPP--------PP------P---------PP*1(1)
2547316QS---------P--------P---------PP---------P--------P---------PP*1(1)
3271546QS--------PP--------PP*1(1)

This set of blocks includes the 12:1+21 block block from 78 complete B-blocks, so the other two blocks link 8 B-blocks into 2 blocks.

• CompLib 94761 582 bobs

2314567QS---------P--------P-P--------P---------P-P--------PP-------P---------PP-------PP---------PPP--------PP------P---------PP*1(1)
1632547QS---------P--------P---------PP---------P--------P---------PP*1(1)
6245137QS-------PP--------PP-*1(1)

no peal

67 round blocks, signature: 22:5+45

2314567QS---------P--------PP---------P--P---------P--PP-PP---------P-P---------P-------P*1(1)
1356742QS---------P--P--PP--P--P---------P--PP--------PP--P*1(1)
1374562QS---------P--P--PP--P------P--------PP--P*1(1)
1547362QS--------P--P---PP--------PP-P-*1(1)
3265714QS--------P--P------P-*1(1)

no peal

67 round blocks, signature: 21:6+45

2314567QS---------P-----P---------PP---------P--------P---------P---P*1(1)
5236147QS---------P--P--PP--P--P---------P--PP--------PP--P*1(1)
7163254QS--------P--PP--------P------P--PP--P--P-*1(1)
7236154QS---------P----PP--------PPP--P*1(1)
7214356QS---------P--P---------P--PP--P*1(1)
2541367QS--------P--P------P-*1(1)

69 round blocks, signature: 20:5+33

2314567QS---------P--------P---------P---P---------P------P---------P--P---------P------P--------P---------PP*1(1)
1356427QS---------P--P---------P--PP--P*1(1)
6351472QS---------P--P---------P--PP--P*1(1)
5246317QS--------PP--------PP*1(1)
3421576QS--------PP--------PP*1(1)

69 round blocks, signature: 18:3+33

2314567QS---------P--------P--------PPP---------P--------P-------PPP--------P---------PPP--------PP------P---------PP---------PP--------P--------P-PP*1(1)
5213647QS--------PP--------PP*1(1)
5234617QS--------PP--------PP*1(1)

• CompLib 82304 642 bobs
• CompLib 86671 576 bobs

69 round blocks, signature: 20:5+33

2314567QS---------P------PP---------PPP------P--P--------P--------P---------PP---------PP*1(1)
2547316QS---------P--------P---------PP---------P--------P---------PP*1(1)
2341576QS---------P------P--P*1(1)
2761534QS--------P-------P-PP*1(1)
5371246QS--------PP--------PP*1(1)

69 round blocks, signature: 21:6+33

2314567QS---------P-----P---------P---P---------P--P---------P------P*1(1)
7356124QS---------P--P---------P------P---------P--P---------P------P*1(1)
6173245QS--------P--PPP--------PP----P-*1(1)
1247635QS---------P------P--P*1(1)
6174532QS--------P--P------P-*1(1)
3146527QS--------PP--------PP*1(1)

69 round blocks, signature: 20:5+33

2314567QS---------P---PP--P---------P--P--------P---------PP---------P--------P*1(1)
3214657QS---------P--P---------P------P---------P--P---------P------P*1(1)
5267143QS---------P--P---------P--PP--P*1(1)
2145637QS--------PP--------PP*1(1)
2743165QS-------PP--------PP-*1(1)

71 round blocks, signature: 20:7+33

2314567QS---------P--------P---------P---P---------P--PP--P--------P---------PP*1(1)
1356427QS---------P--P---------P--PP--P*1(1)
3542716QS---------P------P--P*1(1)
6351472QS---------P------P--P*1(1)
1465327QS--------P--P------P-*1(1)
3724516QS--------P--P------P-*1(1)
5246317QS--------PP--------PP*1(1)

2314567QS---------P--------P---------P---P---------P--PP--P--------P---------PP*1(1)
6351472QS---------P--P---------P--PP--P*1(1)
3456127QS---------P------P--P*1(1)
7342516QS---------P------P--P*1(1)
3165427QS--------P--P------P-*1(1)
2574361QS--------P--P------P-*1(1)
5246317QS--------PP--------PP*1(1)

2314567QS---------P--------P---------P---P--P---------PP--P--------P---------PP*1(1)
3175624QS--------P--P--P---------P--PP-*1(1)
3217564QS---------P------P--P*1(1)
3657124QS---------P------P--P*1(1)
3571264QS--------P--P------P-*1(1)
2574361QS--------P--P------P-*1(1)
5246317QS--------PP--------PP*1(1)

2314567QS---------P--------P---------P-P---------P--P--P--P--------P---------PP*1(1)
3241675QS---------PP---------P--P--P--P*1(1)
1236457QS---------P------P--P*1(1)
2345716QS---------P------P--P*1(1)
1463257QS--------P--P------P-*1(1)
2574361QS--------P--P------P-*1(1)
2463517QS-------PP--------PP-*1(1)

2314567QS---------P--------P---------P-P---------P--P--P--P--------P---------PP*1(1)
3246157QS---------PP---------P--P--P--P*1(1)
7325416QS---------P------P--P*1(1)
3241675QS---------P------P--P*1(1)
3164257QS--------P--P------P-*1(1)
7452316QS--------P--P------P-*1(1)
2463517QS-------PP--------PP-*1(1)

2314567QS---------P--------P---------P-P--P---------P--P--P--------P---------PP*1(1)
6137254QS---------P--P--P---------PP--P*1(1)
3571264QS--------P--P------P-*1(1)
6273154QS--------P--P------P-*1(1)
2574361QS--------P--P------P-*1(1)
6372451QS--------P--P------P-*1(1)
2463517QS-------PP--------PP-*1(1)

2314567QS---------P--------P---------P-P--P---------P--P--P--------P---------PP*1(1)
6372451QS--------P--P--P---------P--PP-*1(1)
2157463QS---------P------P--P*1(1)
1267453QS---------P------P--P*1(1)
2475163QS--------P--P------P-*1(1)
2574361QS--------P--P------P-*1(1)
2463517QS-------PP--------PP-*1(1)

2314567QS---------P-------P---------P--P---------P--P--P--P-------P---------P-P*1(1)
4213675QS---------PP---------P--P--P--P*1(1)
3246157QS---------P------P--P*1(1)
2415736QS---------P------P--P*1(1)
3164257QS--------P--P------P-*1(1)
2571463QS--------P--P------P-*1(1)
2164537QS------P-P-------P-P-*1(1)

2314567QS---------P-------P---------P--P---------P--P--P--P-------P---------P-P*1(1)
4216357QS---------PP---------P--P--P--P*1(1)
7425136QS---------P------P--P*1(1)
4213675QS---------P------P--P*1(1)
4361257QS--------P--P------P-*1(1)
7152436QS--------P--P------P-*1(1)
2164537QS------P-P-------P-P-*1(1)

2314567QS---------P-------P---------P--P--P---------P--P--P-------P---------P-P*1(1)
6472153QS--------P--P--P---------P--PP-*1(1)
2357164QS---------P------P--P*1(1)
3267154QS---------P------P--P*1(1)
2175364QS--------P--P------P-*1(1)
2571463QS--------P--P------P-*1(1)
2164537QS------P-P-------P-P-*1(1)

2314567QS---------P-----P------P------P---------P--P---------P------P*1(1)
7356124QS---------P--P---------P--PP--P*1(1)
6357142QS---------P--P---------P--PP--P*1(1)
6173245QS--------P--P------P-*1(1)
6123754QS--------P--P------P-*1(1)
6154372QS--------P--P------P-*1(1)
3146527QS--------PP--------PP*1(1)

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
3214657QS---------P--P---------P--PP--P*1(1)
5267143QS---------P--P---------P--PP--P*1(1)
4213675QS---------P------P--P*1(1)
2165734QS---------P------P--P*1(1)
2756134QS--------P--P------P-*1(1)
2743165QS-------PP--------PP-*1(1)

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
3214657QS---------P--P--P---------PP--P*1(1)
3764152QS---------P--P--P---------PP--P*1(1)
1542637QS--------P--P------P-*1(1)
3146752QS--------P--P------P-*1(1)
6547132QS--------P--P------P-*1(1)
2743165QS-------PP--------PP-*1(1)

2314567QS---------P---P--P---------P--PP--------P---------PP---------P--------P*1(1)
3214657QS---------P--P--P---------PP--P*1(1)
7134256QS---------P------P--P*1(1)
1754236QS---------P------P--P*1(1)
1542637QS--------P--P------P-*1(1)
1245736QS--------P--P------P-*1(1)
2743165QS-------PP--------PP-*1(1)

2314567QS---------P---PP--P---------P--P--------P---------PP---------P--------P*1(1)
3214657QS---------P--P---------P--PP--P*1(1)
2613475QS---------P------P--P*1(1)
5267143QS---------P------P--P*1(1)
2431675QS--------P--P------P-*1(1)
7156234QS--------P--P------P-*1(1)
2743165QS-------PP--------PP-*1(1)

73 round blocks, signature: 20:9+33

2314567QS---------P-----P------P--PP--P*1(1)
6357142QS---------P--P---------P--PP--P*1(1)
1324657QS---------P------P--P*1(1)
4312576QS---------P------P--P*1(1)
3156724QS---------P------P--P*1(1)
1754623QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
3765124QS--------P--P------P-*1(1)
6142753QS--------P--P------P-*1(1)

2314567QS---------P-----P------P--PP--P*1(1)
6357142QS---------P--P---------P--PP--P*1(1)
4312576QS---------P------P--P*1(1)
3156724QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
6173245QS--------P--P------P-*1(1)
6123754QS--------P--P------P-*1(1)
3765124QS--------P--P------P-*1(1)
6154372QS--------P--P------P-*1(1)

2314567QS---------P-----P------P--PP--P*1(1)
7356124QS---------P--P---------P--PP--P*1(1)
1324657QS---------P------P--P*1(1)
3512476QS---------P------P--P*1(1)
1754623QS---------P------P--P*1(1)
6357142QS---------P------P--P*1(1)
3421576QS--------P--P------P-*1(1)
7165324QS--------P--P------P-*1(1)
6142753QS--------P--P------P-*1(1)

2314567QS---------P-----P------P--PP--P*1(1)
7356124QS---------P--P---------P--PP--P*1(1)
3512476QS---------P------P--P*1(1)
6357142QS---------P------P--P*1(1)
3421576QS--------P--P------P-*1(1)
6173245QS--------P--P------P-*1(1)
6123754QS--------P--P------P-*1(1)
7165324QS--------P--P------P-*1(1)
6154372QS--------P--P------P-*1(1)

2314567QS---------P---P------P--P--P--P*1(1)
3216754QS---------PP---------P--P--P--P*1(1)
4325176QS---------P------P--P*1(1)
3217645QS---------P------P--P*1(1)
4152376QS--------P--P------P-*1(1)
3621475QS--------P--P------P-*1(1)
3761254QS--------P--P------P-*1(1)
3657124QS--------P--P------P-*1(1)
3675142QS--------P--P------P-*1(1)

2314567QS---------P---P------P--P--P--P*1(1)
3216754QS---------PP---------P--P--P--P*1(1)
6514327QS---------P------P--P*1(1)
4325176QS---------P------P--P*1(1)
3217645QS---------P------P--P*1(1)
6274351QS---------P------P--P*1(1)
4152376QS--------P--P------P-*1(1)
3761254QS--------P--P------P-*1(1)
3647521QS--------P--P------P-*1(1)

2314567QS---------P---P------P--P--P--P*1(1)
3217645QS---------PP---------P--P--P--P*1(1)
2315476QS---------P------P--P*1(1)
7236154QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
3621475QS--------P--P------P-*1(1)
7163254QS--------P--P------P-*1(1)
3657124QS--------P--P------P-*1(1)
3675142QS--------P--P------P-*1(1)

2314567QS---------P---P------P--P--P--P*1(1)
3217645QS---------PP---------P--P--P--P*1(1)
6514327QS---------P------P--P*1(1)
2315476QS---------P------P--P*1(1)
7236154QS---------P------P--P*1(1)
6274351QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
7163254QS--------P--P------P-*1(1)
3647521QS--------P--P------P-*1(1)

73 round blocks, signature: 21:10+33

2314567QS---------P--P---------P--PP--P*1(1)
2341576QS---------P------P--P*1(1)
6351724QS---------P------P--P*1(1)
2736514QS---------P------P--P*1(1)
6357142QS---------P------P--P*1(1)
4632571QS---------P------P--P*1(1)
2543617QS--------P--P------P-*1(1)
5216374QS--------P--P------P-*1(1)
6715324QS--------P--P------P-*1(1)
4523671QS--------P--P------P-*1(1)

2314567QS---------P--P---------P--PP--P*1(1)
4312576QS---------P------P--P*1(1)
3156724QS---------P------P--P*1(1)
5721463QS---------P------P--P*1(1)
6357142QS---------P------P--P*1(1)
5376421QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
3765124QS--------P--P------P-*1(1)
4516723QS--------P--P------P-*1(1)
4523671QS--------P--P------P-*1(1)

73 round blocks, signature: 20:9+33

2314567QS---------P--P--P---------PP--P*1(1)
1643527QS--------P--P---P------P--P--P-*1(1)
3274561QS---------P------P--P*1(1)
3654721QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
3741526QS--------P--P------P-*1(1)
3714562QS--------P--P------P-*1(1)
3547261QS--------P--P------P-*1(1)
3765241QS--------P--P------P-*1(1)

2314567QS---------P--P--P---------PP--P*1(1)
2541367QS--------P--P-----P------P--PP-*1(1)
7124365QS---------P------P--P*1(1)
1764325QS---------P------P--P*1(1)
1643527QS--------P--P------P-*1(1)
7351426QS--------P--P------P-*1(1)
7326145QS--------P--P------P-*1(1)
1346725QS--------P--P------P-*1(1)
7341562QS--------P--P------P-*1(1)

2314567QS---------P--P--P---------PP--P*1(1)
3745621QS--------P--P-----P------P--PP-*1(1)
3274561QS---------P------P--P*1(1)
3654721QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
1632547QS--------P--P------P-*1(1)
1645723QS--------P--P------P-*1(1)
1675432QS--------P--P------P-*1(1)
3547261QS--------P--P------P-*1(1)

2314567QS---------P--P--P---------PP--P*1(1)
7342165QS--------P--P---P------P--P--P-*1(1)
7124365QS---------P------P--P*1(1)
1764325QS---------P------P--P*1(1)
2531647QS--------P--P------P-*1(1)
1643527QS--------P--P------P-*1(1)
2574136QS--------P--P------P-*1(1)
1346725QS--------P--P------P-*1(1)
2547163QS--------P--P------P-*1(1)

73 round blocks, signature: 21:10+33

2314567QS---------PP---------P--P--P--P*1(1)
2413576QS---------P------P--P*1(1)
3217645QS---------P------P--P*1(1)
7213654QS---------P------P--P*1(1)
2176534QS---------P------P--P*1(1)
2165473QS---------P------P--P*1(1)
2546137QS--------P--P------P-*1(1)
5231674QS--------P--P------P-*1(1)
7631254QS--------P--P------P-*1(1)
2456173QS--------P--P------P-*1(1)

• CompLib 94745 591 bobs

73 complete B-block peals

All of these sets of blocks here give peals, but I have just shown some peals as an illustration.

67 round blocks

Signature: 21:4+33

2314567QS---------P--------P---------P------P---------P---P---------P-----P---------P---P--------P---------PP*1(1)
4163527QS--------P-----P---------P---P---------P-----P---------P---P-*1(1)
2173546QS-------PP--P---P-----P---P-PP-*1(1)
4215376QS----P---P-----P---P-*1(1)

• CompLib 82297 573 bobs

2314567QS---------P-------P---------P-------P---------P---P---------P-----P---------P---P-------P---------P-P*1(1)
1364527QS--------P-----P---------P---P---------P-----P---------P---P-*1(1)
2173546QS------P-P--P---P-----P---PP-P-*1(1)
1235476QS----P---P-----P---P-*1(1)

69 round blocks

Signature: 21:6+33

2314567QS---------P-----P---------P---P---------P-----P---------P---P*1(1)
1673542QS--------P--------P------P---P---------P-----P---------P---P-*1(1)
4526173QS--------P--PP---P-----P---P-P-*1(1)
4562137QS--------P--P------P-*1(1)
4531726QS--------P--P------P-*1(1)
6512374QS-----P---P-----P---P*1(1)

2314567QS---------P-----P---------P---P---------P-----P---------P---P*1(1)
1763524QS--------P--------P------P---P---------P-----P---------P---P-*1(1)
2547163QS--------P--PP---P-----P---P-P-*1(1)
2531647QS--------P--P------P-*1(1)
2574136QS--------P--P------P-*1(1)
6512374QS-----P---P-----P---P*1(1)

2314567QS---------P-----P------P------P---------P--P---------P------P*1(1)
7356124QS---------P--P---------P------P---------P--P---------P------P*1(1)
1324657QS---------PPP--------PP----P--P*1(1)
1754623QS---------P------P--P*1(1)
6142753QS--------P--P------P-*1(1)
3146527QS--------PP--------PP*1(1)

• CompLib 89127 564 bobs

2314567QS---------P-----P------P------P---------P--P---------P------P*1(1)
7356124QS---------P--P---------P------P---------P--P---------P------P*1(1)
6173245QS--------P--PPP--------PP----P-*1(1)
6123754QS--------P--P------P-*1(1)
6154372QS--------P--P------P-*1(1)
3146527QS--------PP--------PP*1(1)

71 round blocks

Signature: 21:8+33

2314567QS---------P--------P--P-------P---------P-P---------P-------P*1(1)
6172543QS--------P--PP-P-------P-P---P-*1(1)
6521734QS---------P------P--P*1(1)
6527143QS---------P------P--P*1(1)
4653271QS---------P------P--P*1(1)
3245617QS--------P--P------P-*1(1)
6712534QS--------P--P------P-*1(1)
4235671QS--------P--P------P-*1(1)

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
3154627QS---------PPP--------PP----P--P*1(1)
6514327QS---------P------P--P*1(1)
3724651QS---------P------P--P*1(1)
6274351QS---------P------P--P*1(1)
6342157QS--------P--P------P-*1(1)
6345721QS--------P--P------P-*1(1)
3647521QS--------P--P------P-*1(1)

• CompLib 89099 564 bobs
• CompLib 92760 531 bobs
• CompLib 92761 531 bobs, no more than 6 bobs in a row

These two peals have 531 bobs, 45 fewer than any magic block peal, but still considerably more than the 10-part peals. The last peal has 102 Q-sets, but 10 must remain bobbed for the peal to be linked, so unfortunately we can’t remove another 30 bobs from this peal. Perhaps the extra Q-sets make it easier to choose a selection to plain so that there are no more than 6 bobs in a row.

72 complete B-block peals

So far I have 100 sets of blocks made of 72 complete B-blocks and many of them, though not all, give peals. Each sets of blocks has a total of between 67 and 73 round blocks, including B-blocks, to cover the extent. Here are just a few.

67 round blocks, signature: 24:7+45 (a)

2314567QS---------P--------PP---------P------P-PP---------P-P---------P-------P*1(1)
1374562QS---------P--P--PP--P------P--------PP--P*1(1)
2547316QS--------P--PP--------P------P--PP--P--P-*1(1)
1547362QS--------P--P---PP--------PP-P-*1(1)
3756142QS---------P------P--P*1(1)
3265714QS--------P--P------P-*1(1)
3165742QS--------P--P------P-*1(1)

• CompLib 110645 567 bobs

67 round blocks, signature: 24:7+45 (b)

2314567QS---------P--------PP---------P------P-PP---------P-P---------P-------P*1(1)
3756142QS---------PP--P--P--P------P------P--P--P*1(1)
3265714QS--------P--P--P------P------P--P--P--PP-*1(1)
1547362QS--------P--P---PP--------PP-P-*1(1)
1374562QS---------P------P--P*1(1)
2547316QS--------P--P------P-*1(1)
3165742QS--------P--P------P-*1(1)

• CompLib 89701 570 bobs

67 round blocks, signature: 22:5+39

2314567QS---------P------PP--------PPP---------PP------P-P---------PP*1(1)
7526134QS---------PP----P-------P--P---------P--------P------P------P*1(1)
2541367QS--------P-------P---------P-P--P----P---------P-P-*1(1)
2465137QS--------P--P--P---------P--PP-*1(1)
3546217QS--------PP-P-------P*1(1)

• CompLib 94908 582 bobs
• CompLib 93106 570 bobs
• CompLib 89422 576 bobs

67 round blocks, signature: 22:5+33

2314567QS---------P--------P---------P-P---------P--------P---------PP---------P--------P--------P---------PP*1(1)
2541367QS---------P--------P---------PP---------P--------P---------PP*1(1)
3216547QS--------PP--------PP*1(1)
5246317QS--------PP--------PP*1(1)
4652317QS-------PP--------PP-*1(1)

• CompLib 82415 603 bobs

69 round blocks, signature: 23:8+39 (a)

2314567QS---------P-------P---------P--P---------P--P--P--P-------P-P------P---------PP-P*1(1)
4213675QS---------P--P--P---------PP--P*1(1)
2357164QS---------P------P--P*1(1)
5164273QS---------P------P--P*1(1)
1732645QS--------P--P------P-*1(1)
2175364QS--------P--P------P-*1(1)
2571463QS--------P--P------P-*1(1)
2164537QS------P-P-------P-P-*1(1)

• CompLib 94922 570 bobs

69 round blocks, signature: 23:8+39 (b)

2314567QS---------P---P---------P--P--PP---------P--------P*1(1)
3217564QS---------PP---------P--------P---------PP--P-----P*1(1)
6372145QS--------P--P--P---------P--PP-*1(1)
2547163QS---------P------P--P*1(1)
5267143QS---------P------P--P*1(1)
2174563QS--------P--P------P-*1(1)
1653247QS-------PP--------PP-*1(1)
2743165QS-------PP--------PP-*1(1)

• CompLib 111654 564 bobs

69 round blocks, signature: 23:8+39 (c)

2314567QS---------P--------P---------PP--------P---------P-------P---------P-PP*1(1)
5276134QS--------PPP--------PPP------P-*1(1)
2173546QS-------PP-------P--P------PPP-*1(1)
2536417QS--------P--P------P-*1(1)
2571634QS--------P--P------P-*1(1)
5216743QS--------P--P------P-*1(1)
2517643QS--------P--P------P-*1(1)
2546371QS--------P--P------P-*1(1)

• CompLib 111704 558 bobs

71 round blocks, signature: 24:11+39

2314567QS---------P-----P------P--PP--P*1(1)
4567312QS---------P--P--P---------PP--P*1(1)
1324657QS---------P------P--P*1(1)
5631247QS---------P------P--P*1(1)
1754623QS---------P------P--P*1(1)
3274561QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
5213647QS--------P--P------P-*1(1)
6142753QS--------P--P------P-*1(1)
4376512QS--------P--P------P-*1(1)
3547261QS--------P--P------P-*1(1)

• CompLib 94922 570 bobs

71 complete B-block peals

I have found 189 sets of blocks which together with their remaining B-blocks have an odd number of round blocks and can have the sixes rearranged to give 71 complete B-blocks.

63 round blocks, signature: 25:4+42

2314567QS---------P-----P--------PP---P---------P----PPP---------PP----P----P----P--P---------PP---------P--------P--------P----P*1(1)
1642573QS---------P--------P---------PP----P---------P----P---------P----P---------P---P---------PP*1(1)
1436527QS-------PP--------PP-*1(1)
2653174QS----P----P----P----P*1(1)

65 round blocks, signature: 23:4+39

2314567QS---------P--------P-------PPP---------PP-------P-P------PP--------PPP---------P--------P--------P-P---------PP--------P---------PP*1(1)
2516347QS---------P--------P---------PP---------P--------P---------PP*1(1)
5364217QS--------PP--------PP*1(1)
5217463QS--------PP-P-------P*1(1)

2314567QS---------P--------P-------PPP---------PP-------P-P------PP--------PPP---------P--------P--------P-P---------PP--------P---------PP*1(1)
5134267QS---------P-------P---------P-P---------P-------P---------P-P*1(1)
5217463QS--------PP-P-------P*1(1)
5364217QS------P-P-------P-P-*1(1)

• CompLib 82195 549 bobs

2314567QS---------P-----P--------PP---P---------P----PPP---------PP----P----P----P--PP---------P--------P---------PP--------P--------P----P*1(1)
1726534QS---------P----P---------P----P---------P----P---------P----P*1(1)
1572643QS--------PP--------PP*1(1)
2653174QS----P----P----P----P*1(1)

2314567QS---------P-----P--------PP---P---------P----PPP---------PP----P----P----P--PP---------P--------P---------PP--------P--------P----P*1(1)
5167234QS--------P-------P---------P-P---------P-------P---------P-P-*1(1)
1572643QS--------PP--------PP*1(1)
2653174QS-------P-P-------P-P*1(1)

67 round blocks, signature: 25:6+39

2314567QS---------P--------P--------P--------P---------P-P-------P--P------PPP-------P--P-------PPP---------P-------PPP---------P------PP-P*1(1)
5163247QS---------P------P--P*1(1)
2743516QS---------P------P--P*1(1)
5473216QS---------P------P--P*1(1)
2536417QS--------P--P------P-*1(1)
2537146QS--------P--P------P-*1(1)

• CompLib 82166 594 bobs
• CompLib 82157 600 bobs

67 round blocks, signature: 24:7+45

2314567QS---------P--------P--P-------P-P------P---------PP--------P---------PP*1(1)
2431675QS---------PP---P--P------P-----P--P--P--P*1(1)
2163457QS--------P--P--P--P-----P------P--P---PP-*1(1)
2613475QS--------P--P-PP--------PP---P-*1(1)
2436157QS---------P------P--P*1(1)
2516347QS---------P------P--P*1(1)
2561374QS---------P------P--P*1(1)

No peal

67 round blocks, signature: 23:6+51

2314567QS---------P-----P--------PP---P---------P----PPP---------PP----P----P----P--PP---------P--------P---------PP--------P--------P----P*1(1)
5134267QS------P-P--P----P--P-P------PP*1(1)
5143276QS------P-P--P----P--P-P------PP*1(1)
1572643QS--------PP--------PP*1(1)
2653174QS----P-PP-P*1(1)
2754163QS----P-PP-P*1(1)

67 round blocks, signature: 25:8+45

2314567QS---------P---P------P--------P---------PP---------P--------P*1(1)
3146527QS--------PPP--------PPP--P--P-----P------P--P---PP-*1(1)
6514732QS--------P--P--P---------P--PP-*1(1)
2374651QS------P-----P--P------P---P--P*1(1)
3214657QS---------P------P--P*1(1)
3564127QS---------P------P--P*1(1)
2461735QS---------P------P--P*1(1)
6741532QS---------P------P--P*1(1)

No peal

67 round blocks, signature: 23:6+39

2314567QS---------P--P-------P----PP---------P------P------P--------P*1(1)
6514327QS---------P-------P---------P-P---------P----P--P-P*1(1)
3517624QS---------P-------P---------P-P---------P----P--P-P*1(1)
4135276QS---------P--P--P---------PP--P*1(1)
1274365QS--------PP--------PP*1(1)
3145672QS------P----P----P-P-*1(1)

No peal

67 round blocks, signature: 24:7+45

2314567QS---------PP---------P--------PP---------P--P-----P---P--P--P-----P------P--P---PP--------P*1(1)
3217564QS---------PP---P--P------P-----P--P--P--P*1(1)
3157426QS--------PPP--------PPP------P-*1(1)
3215746QS---------P------P--P*1(1)
3475126QS---------P------P--P*1(1)
3457162QS---------P------P--P*1(1)
3175462QS--------P--P------P-*1(1)

No peal

69 round blocks, signature: 24:9+39

2314567QS---------P--------P-------P--P------P-P-------P--P--------P---------PP*1(1)
2461573QS---------P------PPP--------PPP*1(1)
2136547QS---------P------P--P*1(1)
5316247QS---------P------P--P*1(1)
5641273QS---------P------P--P*1(1)
5437261QS---------P------P--P*1(1)
2514763QS--------P--P------P-*1(1)
5217463QS--------P--P------P-*1(1)
2567341QS--------P--P------P-*1(1)

69 round blocks, signature: 23:8+39

2314567QS---------P------PP---------PPP------P--P--------P--------PP---------P--------P---------PPP*1(1)
5134267QS---------P------P--P*1(1)
2341576QS---------P------P--P*1(1)
5431276QS---------P------P--P*1(1)
5376214QS---------P------P--P*1(1)
5367241QS---------P------P--P*1(1)
2761534QS--------P-------P-PP*1(1)
2714536QS--------PP--------PP*1(1)

2314567QS---------P---P------P-P---------P--PP---------P------P------P--------P*1(1)
4135276QS---------P--P--P---------PP--P*1(1)
3675142QS--------P--P------PP------P--P*1(1)
6345172QS---------P------P--P*1(1)
3621475QS--------P--P------P-*1(1)
3657124QS--------P--P------P-*1(1)
3157642QS--------P--P------P-*1(1)
1274365QS--------PP--------PP*1(1)

No peal

2314567QS---------P-----PP---------P--------P---------PP--------P---------P---P*1(1)
1576234QS---------PPP--------PP----P--P*1(1)
1576342QS--------PP---P------P--P----PP*1(1)
1567243QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
2531476QS--------P--P------P-*1(1)
1267534QS--------P--P------P-*1(1)
1276543QS--------P--P------P-*1(1)

• CompLib 110878 546 bobs

70 complete B-block peals

I have found over 2328 sets of an odd number of blocks where the sixes can be rearranged to give 70 complete B-blocks. Some of these can generate peals, and some examples are below.

63 round blocks, signature: 28:7+45

2314567QS---------P-----P---------PP-----P--P------P---P--------P---------P---P*1(1)
2654137QS---------P-------P-P---------P-------P-P---------P-------P-P*1(1)
2541367QS--------P-P-------P---------P-P-------P---------P-P-------P-*1(1)
2145763QS--------P--PPP--------PP----P-*1(1)
2714536QS---------P------P--P*1(1)
2614573QS---------P------P--P*1(1)
2145637QS--------P--P------P-*1(1)

• CompLib 92525 537 bobs
• CompLib 87216 543 bobs

63 round blocks, signature: 26:5+45

2314567QS---------P--------PP---------P------PP--------PPP---------PP-------PP---------P-------PP--------P-P---------P--------PP---------PP*1(1)
5734216QS---------P-------P---------P-P-------P---------P-P---------P-------P-P*1(1)
5246317QS--------PP--------PP*1(1)
5364217QS------P-P-------P-P-*1(1)
5314276QS------P-P-------P-P-*1(1)

• CompLib 90995 546 bobs

67 round blocks, signature: 28:11+45

2314567QS---------P--------P-------P--P------P-PP---------P-P---------P-------P*1(1)
5736124QS---------P---PP--------PP-P--P*1(1)
3756142QS---------P------P--P*1(1)
5736412QS---------P------P--P*1(1)
5736241QS---------P------P--P*1(1)
3756421QS---------P------P--P*1(1)
5163724QS--------P--P------P-*1(1)
3265714QS--------P--P------P-*1(1)
3165742QS--------P--P------P-*1(1)
5463712QS--------P--P------P-*1(1)
3465721QS--------P--P------P-*1(1)

• CompLib 86741 546 bobs, 8 plains in a run
• CompLib 82261 552 bobs, at most 6 bobs in a run
• CompLib 86686 558 bobs, 8 plains in a run, at most 6 bobs in a run

2314567QS---------P--------P---------P-------P---------P-P-------P--P------P-PP*1(1)
5274631QS--------PPP--------PPP------P-*1(1)
2471536QS---------P------P--P*1(1)
5741236QS---------P------P--P*1(1)
2617534QS---------P------P--P*1(1)
5167234QS---------P------P--P*1(1)
2514637QS--------P--P------P-*1(1)
5216437QS--------P--P------P-*1(1)
2514376QS--------P--P------P-*1(1)
2576314QS--------P--P------P-*1(1)
2576431QS--------P--P------P-*1(1)

• CompLib 82116 579 bobs

2314567QS---------P--------P---------P-------P---------P-P-P---------P--P----PP*1(1)
6413275QS--------P--P--PP--------PP--P-*1(1)
5431276QS---------P------P--P*1(1)
3451726QS---------P------P--P*1(1)
6231475QS---------P------P--P*1(1)
3261745QS---------P------P--P*1(1)
5761243QS---------P------P--P*1(1)
6751423QS---------P------P--P*1(1)
3715426QS--------P--P------P-*1(1)
5216743QS--------P--P------P-*1(1)
6415723QS--------P--P------P-*1(1)

• CompLib 82853 582 bobs, 8 plains in a run

67 round blocks, signature 24:7+45

2314567QS---------P--------P-P--------P---------P-P--------PP-------P---------PP-------PP---------PPP--------PP------P---------PP*1(1)
2541367QS--------P-------P-PP*1(1)
2514376QS--------P-------P-PP*1(1)
2517364QS--------P-------P-PP*1(1)
2546371QS--------P-------P-PP*1(1)
2456317QS-------P-P-------P-P*1(1)
3162547QS-------PP--------PP-*1(1)

This set of blocks includes the 12:1+21 block block from 78 complete B-blocks, so the other six blocks link 12 B-blocks into 6 blocks.

• CompLib 119202 588 bobs

69 complete B-block peals

I have found over 600 sets of round blocks which together with some B-blocks give an odd number of round blocks where the sixes can be rearranged to give 69 complete B-blocks. Some of the sets of blocks are given below together with some peals.

57 round blocks (a), signature: 29:2+45

2314567QS---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P*1(1)
1742365QS-------PP--P-----P----P---P----P-----P----P---P----P-----P----P---PPP-*1(1)

• CompLib 77907 582 bobs

57 round blocks (b), signature: 29:2+45

2314567QS---------P-------P---------P-------P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P-------P---------P-P*1(1)
2173546QS------P-P--P----P---P----P-----P----P---P----P-----P----P---P----PP-P-*1(1)

• CompLib 60807 564 bobs
• CompLib 60795 567 bobs
• CompLib 59733 582 bobs
• CompLib 59734 582 bobs
• CompLib 59723 711 bobs
• CompLib 59732 711 bobs
• CompLib 60803 711 bobs
• CompLib 60810 711 bobs with one double omit

59 round blocks, signature: 28:3+45

2314567QS---------P--------P---P-----P---------P---P-----P---------P---P------P---------P--------PP---------P-----P---P---------P-----P---P---------P-----P--PP*1(1)
4516372QS--------P---P-----P---------P---P-----P---------P---P--PP--------PP-P-*1(1)
4561327QS---------P-----P---P---------P-----P---P---------P-----P---P*1(1)

• CompLib 95601 549 bobs

61 round blocks, signature: 27:4+45

2314567QS---------P--------P------PP--------PP-PP---------P--P--------P---------PP---------P--------P---------PP-----P---------PP*1(1)
7356124QS---------P--P---------P-------P---------P-P---------P-------P--------P---------PP---------P--------P*1(1)
5746321QS--------PP------PP--------PPPP*1(1)
2456317QS-------P-P-------P-P*1(1)

• CompLib 95622 597 bobs, 8 plains in a run

63 round blocks, signature: 26:5+45

2314567QS---------P--------P---------PP--------P-P--------P---------P-P--------PP-------P---------PP-------PP---------PPP--------PP------PP*1(1)
2541367QS--------P-------P---------P-P-------P---------P-P---------P-------P-P-*1(1)
3546217QS--------PP--------PP*1(1)
2651347QS-------P-P-------P-P*1(1)
2456317QS-------P-P-------P-P*1(1)

• CompLib 86749 531 bobs
• CompLib 86761 528 bobs

For fewer bobs this peal just beats peals shown previously with 73 and 74 complete B-blocks and 531 bobs. This peal has 4 Q-sets which are bobbed. Plaining them all takes the bob count down to 516, but then there are multiple blocks.

65 round blocks, signature: 25:6+45

2314567QS---------P-----PP---------P--------P---------PP--------P------P--PP--------PP--P*1(1)
5134672QS---------P---P--P---------P--PP--------P---------PP---------P--------P*1(1)
5164732QS---------PPP--------PP----P--P*1(1)
5746132QS--------P--P--P---------P--PP-*1(1)
2654137QS---------P------P--P*1(1)
1542376QS--------PP--------PP*1(1)

• CompLib 95648

67 round blocks, signature: 29:12+45

2314567QS---------P--------P---------P-------P--P--------P---------PP*1(1)
2657431QS---------P---PP--------PP-P--P*1(1)
6217435QS---------P------P--P*1(1)
6347125QS---------P------P--P*1(1)
3217564QS---------P------P--P*1(1)
3657124QS---------P------P--P*1(1)
6471235QS--------P--P------P-*1(1)
6174325QS--------P--P------P-*1(1)
3571264QS--------P--P------P-*1(1)
3175624QS--------P--P------P-*1(1)
2574361QS--------P--P------P-*1(1)
2475631QS--------P--P------P-*1(1)

• CompLib 86680 594 bobs

The peals are also here: - CompLib 69 Stedman Triples bobs-only peals: Complete B-blocks, irregular

68 complete B-block peals

This shows how to arrange the extent so that there are an odd number of round blocks and that the sixes can be rearranged into 68 complete B-blocks. I have found roughly 800 sets of round blocks, and here are a few peals from three of those sets.

55 round blocks, signature: 32:3+57

2314567QS---------P--------P---------PP------P-P--P-----P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P-------P---------P-P---------P-------P---------P-------P---------P----P---------P---P--P-P------PP*1(1)
7532164QS------P-P--P----P---P----P-----P----P---P----P--PPP----PP-P-*1(1)
5724361QS----P-PP-P*1(1)

• CompLib 77861 702 bobs

65 round blocks, signature: 28:9+51

2314567QS---------P---P------P-P---------P--PP---------P------P------P--------P*1(1)
1274365QS--------PP----P-P--P------P-------P--PPP*1(1)
6345172QS---------P------P-P--P------PP*1(1)
4135276QS---------P--P--P---------PP--P*1(1)
3675142QS--------P--P------PP------P--P*1(1)
3621475QS--------P--P------P-*1(1)
6324175QS--------P--P------P-*1(1)
6351724QS--------P--P------P-*1(1)
3657124QS--------P--P------P-*1(1)

• CompLib 88087 600 bobs
• CompLib 77302 573 bobs

71 round blocks, signature: 24:11+45

2314567QS---------P------PPP--------PPP*1(1)
2167543QS-------PP--------PPP------P--P*1(1)
5134267QS---------P------P--P*1(1)
2413576QS---------P------P--P*1(1)
5143276QS---------P------P--P*1(1)
5716234QS---------P------P--P*1(1)
5617243QS---------P------P--P*1(1)
7514236QS--------PP--------PP*1(1)
5234761QS--------PP-P-------P*1(1)
5263741QS--------PP-P-------P*1(1)
5132764QS-------PP--------PP-*1(1)

• CompLib 90280 546 bobs

67 complete B-block peals

I have found over 250 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [61 to 71] of round blocks where the sixes can be rearranged to give 67 complete B-blocks. Some of the sets of blocks are given below together with some peals.

63 round blocks, signature: 30:9+51

2314567QS---------P--------P--------P-P---------P------PPP---------P--------P---------P-P------P-P---------PP*1(1)
5134267QS---------P-------P---------P-P------PP---------P-P*1(1)
2617534QS--------PP------PP--------PPPP*1(1)
5741236QS---------P------P--P*1(1)
2417563QS---------P------P--P*1(1)
5147263QS---------P------P--P*1(1)
2643571QS---------P------P--P*1(1)
5463271QS---------P------P--P*1(1)
5364217QS------P-P-------P-P-*1(1)

• CompLib 86620 561 bobs

67 round blocks, signature: 28:11+45

2314567QS---------P--------P--P-------P---------P--------PP---------P------P-PP*1(1)
4516372QS--------P--P---PP--------PP-P-*1(1)
4561327QS---------P------P--P*1(1)
2561374QS---------P------P--P*1(1)
7361524QS---------P------P--P*1(1)
4361572QS---------P------P--P*1(1)
7561342QS---------P------P--P*1(1)
2516347QS--------P--P------P-*1(1)
4316527QS--------P--P------P-*1(1)
7516324QS--------P--P------P-*1(1)
7316542QS--------P--P------P-*1(1)

• CompLib 96116 549 bobs

66 complete B-block peals

I have found over 84 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [47 to 71] of round blocks where the sixes can be rearranged to give 66 complete B-blocks. Some of the sets of blocks are given below together with some peals.

47 round blocks, signature: 39:2+63

2314567QS---------P-----P---------P----P---------P---P---------P--PP--------PPP*3(1)
6342571QS---------P--------P---------PP---------P--P----P-----P-----P*3(1)

• CompLib 85935 585 bobs, irregular three-part
• CompLib 96222 594 bobs, three-part
• CompLib 86220 591 bobs, three-part

51 round blocks, signature: 36:3+57

2314567QS---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P*1(1)
1742365QS-------PP--P-----P-PP--------PP-P---P----P-----P----P---P----P-----P----P---PPP-*1(1)
7146325QS---------PP---------P--------P---------PP---------P--------P*1(1)

• CompLib 78043 606 bobs

63 round blocks, signature: 32:7+51

2314567QS---------P--------P---------PP------PP--------PPP---------PP------P-PP*1(1)
7521436QS---------PP----P-------P--P---------P--------P------P------P*1(1)
2541367QS--------P-------P---------P-P-------P---------P-P--P----P-P-*1(1)
2615437QS--------P--P--P---------P--PP-*1(1)
3546217QS--------PP--------PP*1(1)
3561247QS--------PP-P-------P*1(1)
2456317QS-------P-P-------P-P*1(1)

• CompLib 88097 612 bobs
• CompLib 91434 573 bobs

Three-part peals

The three-part peals make a change from the one-part peals. There are several types of three-part peals:

Exact three-parts: all the parts are called the same.

Other three-parts:

Blocks which divide the extent into 3 identical parts. These are then linked with Q-sets of bobs or omits. For an easier peal it is best to use only 1 Q-set (or perhaps a second at a similar point in other parts). The sixes affected by the Q-set should be as close a possible to minimise the disruption. If the 3 identical parts are divided into ABCD at the Q-set points then peals of the form ABC'CDAB'BCA'D where ‘ is a bob or omit can sometimes be found. We should minimise the length of B and C. So the peal links the parts like this:

1234567: ABC
           /
1357246: ..CD
1357246: AB
          /
1526374: .BCD
1526374: A
          \
           \
1234567: ...D

A variation is AB'B'BC'C'CDA'DA'D which might be easier to call, at the expense of a longer first part and shorter second and third parts.

It might be possible to add extra Q-sets of omits to reduce the bob count, but the peal is then less regular.

Sometime the extent can be split into round blocks using a group of order 3, but not into 3 identical parts, but in 2,3,4,5.. sets of 3 identical parts. If there are an odd number of sets then it might be possible to find some Q-sets of bobs or omits to link everything together.

Irregular three-parts

By bobbing all available Q-sets there might be whole B-blocks revealed as some of the sets. If complementary pairs of B-blocks are then available a free choice of 1 of the 6 possible pairs can be made, and that might give more Q-sets of omits to link everything together. The result is going to be a much less regular peal though.

With all these three-part peals then by choosing an appropriate rotation/reversal a good part-end (either 1357246 or 3456127 etc.) can often be found.

65 complete B-block peals

I have found 25 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [53 to 63] of round blocks where the sixes can be rearranged to give 65 complete B-blocks. I have found two of the sets of blocks give some peals.

53 round blocks, signature: 35:4+57

2314567QS---------P-----P---------P-----P---------P----P---------P---P---------P----P-----PP---------P--------P---------PP--------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P*1(1)
1742365QS-------PP--P-----P----P---P----P-----P----P---P----P-----P----P---PPP-*1(1)
2451376QS-------P---P-----PP-*1(1)
3652147QS-------PP--------PP-*1(1)

• CompLib 85017 573 bobs

61 round blocks, signature: 35:14+63

2314567QS---------P--------P---------P-------P-P--P------P-------P-P-P--P------P-------PP*1(1)
1324657QS---------P---P-P-P------P--P-----P-PP--P*1(1)
2514376QS---------PP---------P--P--P--P*1(1)
2671435QS---------P------P--P*1(1)
3265714QS---------P------P--P*1(1)
5216743QS---------P------P--P*1(1)
6314572QS---------P------P--P*1(1)
7514362QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
1642357QS--------P--P------P-*1(1)
2417635QS--------P--P------P-*1(1)
6541372QS--------P--P------P-*1(1)
7341562QS--------P--P------P-*1(1)
7235461QS--------P--P------P-*1(1)

• CompLib 96461 585 bobs

64 complete B-block peals

I have found 48 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [51 to 69] of round blocks where the sixes can be rearranged to give 64 complete B-blocks. Here are some of the blocks and some peals.

51 round blocks, signature: 38:5+69

2314567QS---------P--------P---------PP------P-P--P-----P----P-P---------P-------P---------P-P-------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P-------P---------P-P---------P-------P---------P-------P---------P----P---------P---P--P-P------PP*1(1)
7532164QS------P-P--P----P---P----P-----P----P---P----P--PPP----PP-P-*1(1)
1352764QS-------P-P-------P-P*1(1)
1543726QS------P----P----P-P-*1(1)
5724361QS----P-PP-P*1(1)

• CompLib 77951 588 bobs

51 round blocks, signature: 38:5+63

2314567QS---------P-------P---------P-------P---------P----P---------P---P---------P----P---------P-----P----P-P---------P-------P---------P-P-------P---P---------P----P---------PP--P---------P-P---------P-------P---------PP---------P----P-------P---------P-P*1(1)
7346152QS-------P----P---P----P-----P----P---P----PP-P-------P-P--P----P---P-P-*1(1)
3516742QS---------P------P--P*1(1)
5713246QS-------P-P-------P-P*1(1)
5167234QS------P----P----P-P-*1(1)

61 round blocks, signature: 31:8+57

2314567QS---------P------PP--------PPP---------PP-------PP---------P-------PP--------P-P---------P-------P--P------PPP---------PP------P-PP*1(1)
5134267QS---------P-------P---------P-P-------P---------P-P------PP-P*1(1)
2471536QS---------P------P--P*1(1)
5741236QS---------P------P--P*1(1)
5376214QS--------P-------P-PP*1(1)
2514637QS--------P--P------P-*1(1)
5261347QS--------PP-P-------P*1(1)
5364217QS------P-P-------P-P-*1(1)

• CompLib 96536 561 bobs
• CompLib 112212 549 bobs

63 round blocks, signature: 28:7+54

2314567QS---------P-------P------P----P----PP---------PPP----P-P-------P---P--------P---------PP---------PP------P----P----P--P-P*1(1)
1264573QS--------PP------P-P--P----P----P------P-------P--P*1(1)
5174236QS--------P-------P----P-------P*1(1)
1326547QS------P-------P--P------P-P--P*1(1)
5624173QS---------P------P--P*1(1)
5743126QS--------P-------P-PP*1(1)
1723546QS----P-PP-P*1(1)

• CompLib 91460 573 bobs

63 complete B-block peals

I have found 16 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [47 to 63] of round blocks where the sixes can be rearranged to give 63 complete B-blocks. Here are two of the sets of blocks which give some peals. These two sets of blocks happen to come from a three-part group.

47 round blocks, signature: 39:2+63

2314567QS---------P-------P---------P-------P---------P----P---------P---P---------P----P-------P---------P-P*3(1)
2173546QS------P-P--P----P---P----PP-P-*3(1)

• CompLib 38985 705 bobs
• CompLib 72834 588 bobs
• CompLib 38836 600 bobs, three-part
• CompLib 72920 594 bobs, three-part
• CompLib 72887 591 bobs, three-part

47 round blocks, signature: 39:2+63

2314567QS---------P-----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P*3(1)
5126347QS-------PP--P-----P----P---PPP-*3(1)

• CompLib 37434 582 bobs

62 complete B-block peals

I have found 25 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [45 to 69] of round blocks where the sixes can be rearranged to give 62 complete B-blocks. Here are 7 of the sets of blocks which give some peals.

45 round blocks, signature: 42:3+69

2314567QS---------P--------P---------PP---------P--------P-P----P---------P---P---------P----P---------P-----P---------P----P---------P---P-P-P---------P-------P---------P-P---------P-------P-------P----P---------P-----P---------P-----P---------P---PP--------PP---P---------PP---------P--------P---P---------P----P---------P-----P-------PP*1(1)
6724531QS-------PPP---P----P-----P----P---P----P-----P----P---P----P-----P--PP-*1(1)
5364217QS------P-P-------P-P-*1(1)

• CompLib 85502 588 bobs

49 round blocks, signature: 42:7+69

2314567QS---------P-----P---------P-----P---------P----P-------P--P------P-P---P---------P----P---------P-----P---------P----P---------P---P---------P----P-P------P--P-------P-----P---------P----P---------P---P--------P---------PP---------P---P--P---------P-P*1(1)
1742365QS-------PP--P-----P----P---P----P-----P----P---P----P-----P----P---PPP-*1(1)
5672143QS---------P------P--P*1(1)
7134562QS---------P------P--P*1(1)
5167234QS--------P--P------P-*1(1)
5127643QS--------P--P------P-*1(1)
7543162QS--------P--P------P-*1(1)

57 round blocks, signature: 40:13+66

2314567QS---------P-------P---------P-PPP--------PP----PP---------P-P*1(1)
1426357QS---------P-----P------P------P---------P--P---------P------P*1(1)
1726534QS---------P----P---------P----P---------P----P--P-P*1(1)
7435216QS---------P--P---------P---P--P--P---------P------P*1(1)
7541326QS---------P------P--P*1(1)
7514362QS---------P------P--P*1(1)
3672541QS---------P------P--P*1(1)
1574263QS--------P-------P-PP*1(1)
7314526QS--------P--P------P-*1(1)
7341562QS--------P--P------P-*1(1)
3527641QS--------P--P------P-*1(1)
4265317QS--------PP--------PP*1(1)
1247563QS------P----P----P-P-*1(1)

59 round blocks, signature: 32:7+59

2314567QS---------P--------P---------P-------P-------P---------P-P--P----P---------P---P-----P---------P-PPP--------PPP----P---------P----P------P-PP*1(1)
4721536QS---------P-------P------P----P---------P----P--P-P*1(1)
6127534QS---------P-------P------P----P---------P----P--P-P*1(1)
4651237QS-------P-P----P----P*1(1)
6457231QS-------P-P----P----P*1(1)
2541673QS------P----P----P-P-*1(1)
2567413QS------P----P----P-P-*1(1)

• CompLib 81821 642 bobs

59 round blocks, signature: 40:15+66

2314567QS---------P---P------P--------P---------P---P--P---------P--P---P-----P*1(1)
2451376QS--------P-----P---P---------P--P--P---P---------P-----P--PP-*1(1)
3652471QS--------P--P-P---P-----P---PP-*1(1)
2435617QS---------P------P--P*1(1)
6345217QS---------P------P--P*1(1)
1675324QS---------P------P--P*1(1)
2175643QS---------P------P--P*1(1)
6715243QS---------P------P--P*1(1)
3425671QS---------P------P--P*1(1)
4375621QS---------P------P--P*1(1)
1357624QS--------P--P------P-*1(1)
2654713QS--------P--P------P-*1(1)
6257413QS--------P--P------P-*1(1)
4657321QS--------P--P------P-*1(1)
2743165QS----P---P-----P---P-*1(1)

63 round blocks, signature: 28:7+57

2314567QS---------P---P-------P-P------PP------P-P-------P--P-------P---------PPP----P--PPP--------PP----P----P------P-P--------P*1(1)
3254671QS--------P--P-------P------P----P----P--P-P------PP*1(1)
2651347QS--------P-------P----P-------P*1(1)
2314675QS--------P-------P----P-------P*1(1)
6537241QS-------P------P--P-P------P--P*1(1)
6731245QS----P-PP-P*1(1)
3567214QS----P-PP-P*1(1)

• CompLib 112214 582 bobs
• CompLib 112244 570 bobs

69 round blocks, signature: 28:13+57

2314567QS---------P----PP--------PPP--P*1(1)
6345172QS-------PP------P------P--P-PP-*1(1)
2413576QS---------P------P--P*1(1)
1523647QS--------PP--------PP*1(1)
1632547QS--------PP--------PP*1(1)
1624537QS--------PP--------PP*1(1)
1573624QS--------PP--------PP*1(1)
1642573QS--------PP--------PP*1(1)
1345627QS-------PP--------PP-*1(1)
6435127QS-------PP--------PP-*1(1)
1725643QS-------PP--------PP-*1(1)
2536174QS-----P--P------P--P-*1(1)
3675142QS-----P--P---P-----P-*1(1)

• CompLib 112259 552 bobs

61 complete B-block peals

I have found 173 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [43 to 57] of round blocks where the sixes can be rearranged to give 61 complete B-blocks. Here are 4 of the sets of blocks together with some peals.

43 round blocks, signature: 45:4+72

2314567QS---------P---------PP---------P-----P---------P----P---------P---P---------P----P-----PP---------P--------P---------PP---------P--------P---P-----P---------P-----P---------P--------P---------PP---------P--------P---P---------P----P---------P-----P---------P----P---P--------P---------PP---------P--------P---------PP-----P---P---------P---P*1(1)
3462157QS-------PPP---P----P-----P----P---P----P-----P----P---P----P-----P--PP-*1(1)
4715236QS-----P--P------P--P-*1(1)
1537264QS-----P--P------P--P-*1(1)

45 round blocks, signature: 43:4+69

2314567QS---------P--------P---------PP---------P--------P---P-----P---------P-----P---------P--------P---------PP---------P--------P---P---------P----P---------P-----P---------P----P---P--------P---------PP---------P--------P---------PP-----P---P---------P----P---------P-----P---------P----P---------P---P---------P----P-----PP*1(1)
7642153QS-------PPP---P----P-----P----P---P----P-----P----P---P----P-----P--PP-*1(1)
4563217QS-----P--P------P--P-*1(1)
6315274QS-----P--P------P--P-*1(1)

• CompLib 77906 621 bobs

45 round blocks, signature: 43:4+69

2314567QS---------P--------P---------PP---------P--------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P-P-P---------P-------P---------P-P---------P-------P------P---------PP---------P--------P---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P----PP*1(1)
2456731QS-------PP--P-----P----P---P----P-----P----P---P----P-----P----P---PPP-*1(1)
3546217QS--------PP--------PP*1(1)
2456317QS-------P-P-------P-P*1(1)

• CompLib 78110 585 bobs, 8 plains in a row

49 round blocks, signature: 43:8+93

2314567QS---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P----PP------P-P--P----P--P-P-P----P---------P---P---------P----P---------P-----P---------P----P---------P---P-P-P--P----P--P-P------PP---P---------PP---------P--------P*1(1)
1742365QS-------PP--P-----P----P---P----P-----P----P---P----P-----P----P---PPP-*1(1)
1423675QS------P-P--P----P--P-P------PP*1(1)
1675432QS------P-P--P----P--P-P------PP*1(1)
4215637QS----P-PP-P*1(1)
4317625QS----P-PP-P*1(1)
1742653QS----P-PP-P*1(1)
1543672QS----P-PP-P*1(1)

• CompLib 85496 576 bobs, 8 plains in a row

2314567QS---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P----P--P------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P-P--P------P------P---------PP---------P--------P*1(1)
1742365QS-------PP--P-----P----P---P----P-----P----P---P----P-----P----P---PPP-*1(1)
1632475QS--------P--P------P-*1(1)
6134275QS--------P--P------P-*1(1)
1674523QS--------P--P------P-*1(1)
6175423QS--------P--P------P-*1(1)
1654732QS--------P--P------P-*1(1)
6157432QS--------P--P------P-*1(1)

• CompLib 112281 570 bobs

60 complete B-block peals

I have found 6 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [47 to 59] of round blocks where the sixes can be rearranged to give 60 complete B-blocks. Here are the sets of blocks together with a peal.

47 round blocks, signature: 46:9+81

2314567QS---------P--------P---------PP------P-P--P-----P---------P----P---------P---P----P------P--P----P----P---------P-----P---------P----P---------P---P---------P----P-------P---------P-P---------P-------P---------P-------P-------P------P--P-P----P---------P---P--P-P------PP*1(1)
7532164QS------P-P--P----P---P----P-----P----P---P----P--PPP----PP-P-*1(1)
4731625QS---------P------P--P*1(1)
6371425QS---------P------P--P*1(1)
6413527QS--------P--P------P-*1(1)
4615327QS--------P--P------P-*1(1)
6412735QS--------P--P------P-*1(1)
4617235QS--------P--P------P-*1(1)
5724361QS----P-PP-P*1(1)

Gives peals, but similar to blocks below

47 round blocks, signature: 46:9+81

2314567QS---------P--------P---------PP------P-P--P-----P---------P----P---------P---P-P--P------P-------P----P---------P-----P---------P----P---------P---P---------P----P-------P---------P-P---------P-------P---------P-------P----P--P------P----P----P---------P---P--P-P------PP*1(1)
7532164QS------P-P--P----P---P----P-----P----P---P----P--PPP----PP-P-*1(1)
4351627QS---------P------P--P*1(1)
6531427QS---------P------P--P*1(1)
4271635QS---------P------P--P*1(1)
6721435QS---------P------P--P*1(1)
4613725QS--------P--P------P-*1(1)
6417325QS--------P--P------P-*1(1)
5724361QS----P-PP-P*1(1)

• CompLib 77124 582 bobs

59 round blocks, signature: 43:18+75

2314567QS------P-----P--P-----P------P--P---PP--P*1(1)
1435672QS--------P--P------PP------P--P*1(1)
1653472QS--------P--P------PP------P--P*1(1)
2374165QS--------P--P--P---------P--PP-*1(1)
4567312QS------P-----P--P------P---P--P*1(1)
2463517QS------P--P-----P------P--P---P*1(1)
5631247QS---------P------P--P*1(1)
2147365QS---------P------P--P*1(1)
3672154QS---------P------P--P*1(1)
5427163QS---------P------P--P*1(1)
3274561QS---------P------P--P*1(1)
2541367QS--------P--P------P-*1(1)
5213647QS--------P--P------P-*1(1)
5271436QS--------P--P------P-*1(1)
3127654QS--------P--P------P-*1(1)
3547261QS--------P--P------P-*1(1)
5276341QS--------P--P------P-*1(1)
6724531QS--------P--P------P-*1(1)

No peals

59 complete B-block peals

I have found 6 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [45 to 55] of round blocks where the sixes can be rearranged to give 59 complete B-blocks. Here is one set of blocks which gives a peal.

47 round blocks, signature: 44:7+75

2314567QS---------P-----P---------P-----P---P------P--P-----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P------P--PP----P---------P-----P---------P----P---------P---P--------P---------PP--------P------P--PP--------P*1(1)
1742365QS-------PP-P--P------PP-----P----P---P----P-----P--P--P------P-P---P----P-----P----P---PPP-*1(1)
6137254QS---------P------P--P*1(1)
6271453QS--------P--P------P-*1(1)
2674153QS--------P--P------P-*1(1)
2645731QS--------P--P------P-*1(1)
6247531QS--------P--P------P-*1(1)

• CompLib 85051 597 bobs

58 complete B-block peals

I have found 67 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [39 to 69] of round blocks where the sixes can be rearranged to give 58 complete B-blocks. Several sets of the blocks give peals, here are two together with some peals.

45 round blocks, signature: 50:11+99

2314567QS---------P---P----P--P------P----P--P---------P------P------P------PP--P---------P--P--P-P*1(1)
4271635QS--------P-------P---------P-P---------P-------P---------P-P-*1(1)
4617235QS--------P-------P---------P-P---------P-------P---------P-P-*1(1)
4235716QS--------P--PP--P----P--P----PP--------PPP----P--P-*1(1)
4135276QS---------P--P--P--P--P------P------PP--P*1(1)
4153672QS---------P--P--P--P--P------P------PP--P*1(1)
4735612QS---------P--P--P--P--P------P------PP--P*1(1)
4635172QS--------P--PP--P----P--P------P----P--P-*1(1)
4653712QS--------P--PP--P----P--P------P----P--P-*1(1)
4163275QS-------P-P-------P-P*1(1)
4723615QS-------P-P-------P-P*1(1)

• CompLib 81638 585 bobs
• CompLib 81616 591 bobs
• CompLib 82045 624 bobs

63 round blocks, signature: 28:7+57

2314567QS---------P---P-------P------P----P------P-------P--P-------P---------PP-----P--P--------P--P-------PPP--------PP----P----P------P-P--------P*1(1)
2645317QS--------P--P-------P------P----P------P-------P--P*1(1)
3254671QS--------P--P-------P------P----P------P-------P--P*1(1)
6731245QS----P-PP-P*1(1)
2167354QS----P-PP-P*1(1)
3567214QS----P-PP-P*1(1)
6725341QS----P-PP-P*1(1)

• CompLib 89492 564 bobs

57 complete B-block peals

I have found 5 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [41 to 55] of round blocks where the sixes can be rearranged to give 57 complete B-blocks. Two of the sets of the blocks give peals which are illustrated below.

41 round blocks, signature: 49:6+81

2314567QS---------P-----P---------P-----P---------P----P---------P---P---------P----P-----PP---------P--------P---------PP--------P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P*1(1)
4612537QS---------P--------P---------PP---------P--------PP-----P----P---P----P-----P--P-P---------P-------P---------P-P---------P-------P-P---PPP--------PP--P-----P----P---P---PP*1(1)
6523417QS--------PP--------PP*1(1)
2451376QS-------P---P-----PP-*1(1)
4253617QS-------P-P-------P-P*1(1)
3652147QS-------PP--------PP-*1(1)

• CompLib 85910 609 bobs

55 round blocks, signature: 47:18+81

2314567QS---------P---P------P--------P----P--P------P----PP-P--P------P-------P--------P*1(1)
1234756QS--------P--P------PP------P--P*1(1)
1743256QS--------P--P------PP------P--P*1(1)
6372451QS--------P--P------PP------P--P*1(1)
6427351QS--------P--P------PP------P--P*1(1)
6273541QS--------P--PPP--------PP----P-*1(1)
3214657QS---------P------P--P*1(1)
1523476QS---------P------P--P*1(1)
1574326QS---------P------P--P*1(1)
7362154QS---------P------P--P*1(1)
2467153QS---------P------P--P*1(1)
4713652QS---------P------P--P*1(1)
6537241QS---------P------P--P*1(1)
6542731QS---------P------P--P*1(1)
1347526QS--------P--P------P-*1(1)
2176453QS--------P--P------P-*1(1)
4631752QS--------P--P------P-*1(1)
6724531QS--------P--P------P-*1(1)

• CompLib 81744 603 bobs

56 complete B-block peals

I have found 144 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [35 to 61] of round blocks where the sixes can be rearranged to give 56 complete B-blocks. Only two of the sets of the blocks give peals which are illustrated below.

55 round blocks, signature: 42:13+81

2314567QS---------P-------P---------P--P--P---------P--P--P-------P---------P-P*1(1)
7216345QS------P--P----P----P------PP--P-P-------P-P-P-P--P----P----P*1(1)
1572364QS-------P------P--P-P-------P------P-P--P----P--P-P*1(1)
7356124QS--------P--P------PP------P-P--P------PP*1(1)
7165324QS------P--P------P-P--P----P--P------P-P-*1(1)
3615247QS---------P------P--P*1(1)
4156327QS---------P------P--P*1(1)
3251647QS--------P--P------P-*1(1)
4365127QS--------P--P------P-*1(1)
2571463QS--------P--P------P-*1(1)
6472153QS--------P--P------P-*1(1)
1432765QS-------P-P----P----P*1(1)
7345126QS------P----P----P-P-*1(1)

• CompLib 92618 612 bobs
• CompLib 92614 618 bobs
• CompLib 87958 627 bobs

61 round blocks, signature: 32:9+69

2314567QS---------P--P--P----P--P-P------PP-----PP---------P--P--P------P------P--------P*1(1)
3215746QS---------PP-----PP------P-P--P----P--P-PP--P--P--P*1(1)
1274365QS--------PP------P-------P----P-------PPP*1(1)
3627145QS--------P-------P----P-------P*1(1)
3124675QS------P-P--P----P--P-P------PP*1(1)
3675142QS------P-P--P----P--P-P------PP*1(1)
3217564QS---------P------P--P*1(1)
1437625QS-------P-P----P----P*1(1)
6345172QS------P----P----P-P-*1(1)

• CompLib 97256 603 bobs

55 complete B-block peals

I have found 32 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [35 to 59] of round blocks where the sixes can be rearranged to give 55 complete B-blocks. The two sets of blocks which give peals are illustrated below.

37 round blocks, signature: 52:5+87

2314567QS---------P--------P-P-------PP---------PPP-------P---------PPP-----P---P---------P----P---------P-----P---------P-----P---------P--------P---------PP---------P--------P---P---------P----P---------P-----P---------P----P---------P---P---------P----P--------PP---------P--------P---------PP-----P----P--P--------P---------P-P--------P--------P*1(1)
2671354QS---------P--------P---------PP---P---P----P-----P--PP--------PPP---P----P-----P----P---P----P-----PP--------P---------PP*1(1)
3274615QS--------PP--------PP*1(1)
5124763QS-------PP--------PP-*1(1)
7625431QS-------PP-----P---P-*1(1)

• CompLib 85460 600 bobs
• CompLib 85911 600 bobs
• CompLib 85048 615 bobs

47 round blocks, signature: 44:7+87

2314567QS---------P-------P--------P------P---P---------P-----P---------P---P---------P-----P--P-P--PP--P-----P---------P---P-----P---------P---P------P----PP-P-----P---P------PPP-----P---P------P--------PP--P-----P-PP-P---------P---P---------P-----P---------P---P---------P--P-P-PP-----P---P-----P--PP-----P---P-----PP*1(1)
3465217QS-------PP----P------P--P---PP-*1(1)
3752641QS---------P------P--P*1(1)
7423516QS-------PP-----P---P-*1(1)
7123564QS-------PP-----P---P-*1(1)
5143276QS-----P---P-----P---P*1(1)
2371564QS-----P---P-----P---P*1(1)

• CompLib 92569 591 bobs

54 complete B-block peals

I have found 72 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [33 to 45] of round blocks where the sixes can be rearranged to give 55 complete B-blocks. Some of the sets of blocks which give peals are illustrated below.

35 round blocks, signature: 56:7+93

2314567QS---------P--------P---------PP---------P--------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P----PP*1(1)
6513472QS---------P--------P----PP--P-----P--P-P---------P-------P---------P-P---------P-------P-P---P----PPP--------PP---P----P---P---PP*1(1)
2516347QS---------P--------P---------PP---------P--------P---------PP*1(1)
6531427QS---------P--------PP-----P----P---PPP---PP*1(1)
5412637QS--------PP--------PP*1(1)
3546217QS--------PP--------PP*1(1)
6142537QS-------P-P-------P-P*1(1)

• CompLib 92746 612 bobs

35 round blocks, signature: 54:5+90

2314567QS---------P-----P---------P----P---------P----P---------P----P-P---------P---P---------P----P---------P----P---------P----P-------P*3(1)
3462157QS-------PP-P--P----P----P----PP*3(1)
3621547QS----P----P----P----P*1(1)
3275416QS----P----P----P----P*1(1)
3562174QS----P----P----P----P*1(1)

• CompLib 93332 621 bobs
• CompLib 86279 630 bobs, irregular three-part
• CompLib 93333 645 bobs

These are blocks from a group of order 3 so give irregular, but not exact, three-part peals

39 round blocks, signature: 54:9+105

2314567QS---------P---P----P--P----PP--------PPP----P--P---------P------P------P------PP--P---------P--P--P-P*1(1)
2574361QS---------P---P----P--P----PP--------PPP----P--P---------P------P------P------PP--P---------P--P--P-P*1(1)
6514327QS---------P---P----P--P------P----P--P---------P------P------P------PP--P---------P--P--P-P*1(1)
4271635QS--------P-------P---------P-P---------P-------P---------P-P-*1(1)
4617235QS--------P-------P---------P-P---------P-------P---------P-P-*1(1)
4653712QS--------P--PP--P----P--P----PP--------PPP----P--P-*1(1)
4153672QS---------P--P--P--P--P------P------PP--P*1(1)
4163275QS-------P-P-------P-P*1(1)
4723615QS-------P-P-------P-P*1(1)

These are curious blocks - some are repeated, some are not.

• CompLib 81643 603 bobs

45 round blocks, signature: 54:15+90

2314567QS---------P-----P---------P---P------P--------P---------P---P*1(1)
7613245QS---------P-----P---------P---P------P--------P---------P---P*1(1)
5416732QS---------P-----P---------P---P------P--------P---------P---P*1(1)
1234756QS--------P-----P---------P---P---------P-----P--PP-*1(1)
1763524QS--------P-----P---------P---P---------P-----P--PP-*1(1)
1546273QS--------P-----P---------P---P---------P-----P--PP-*1(1)
4172536QS---------P-P---P-----P---PP--P*1(1)
3157264QS---------P-P---P-----P---PP--P*1(1)
6125743QS---------P-P---P-----P---PP--P*1(1)
4527136QS--------P--P------P-*1(1)
3275164QS--------P--P------P-*1(1)
6752143QS--------P--P------P-*1(1)
1465327QS----P---P-----P---P-*1(1)
1342675QS----P---P-----P---P-*1(1)
1527463QS----P---P-----P---P-*1(1)

• CompLib 86257 663 bobs, three-part Not an exact three-part, but reasonably regular

53 complete B-block peals

I have found 19 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [31 to 59] of round blocks where the sixes can be rearranged to give 53 complete B-blocks. Here is a set of blocks which gives peals.

35 round blocks, signature: 56:7+93

2314567QS---------P--------P---------PP---------P--------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P-P-P---------P-------P---------P-P---------P-------P------P---------PP---------P--------P---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P----PP*1(1)
6513472QS---------P--------P----PP--P-----P--P-P---------P-------P---------P-P---------P-------P-P---P----P-----P----P---P---PP*1(1)
6531427QS---------P--------PP-----P----P---PPP---PP*1(1)
5412637QS--------PP--------PP*1(1)
3546217QS--------PP--------PP*1(1)
6142537QS-------P-P-------P-P*1(1)
2456317QS-------P-P-------P-P*1(1)

• CompLib 92722 594 bobs This peal ends with 7 plain sixes, i.e. half of the plain course.

52 complete B-block peals

I have found 42 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [31 to 35] of round blocks where the sixes can be rearranged to give 52 complete B-blocks. Here is a set of blocks which gives peals.

33 round blocks, signature: 57:6+99

2314567QS---------P--------P---------PP---------P--------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P---PP--------P---------PP---------P--------PP---------PP-P---P----PPP--------PP---P----P---P---PP---------P--------P----PP--P-----P--P-P---------P-------P---------P-P---------P-----P----P---------PP---------P--------P---------P-----P---------P-----P---------P----P---------P---P---------P----P---------P-----P----PP*1(1)
6531427QS---------P--------PP-----P----P---PPP---PP*1(1)
5412637QS--------PP--------PP*1(1)
3546217QS--------PP--------PP*1(1)
6142537QS-------P-P-------P-P*1(1)
3162547QS-------PP--------PP-*1(1)

• CompLib 92729 600 bobs

51 complete B-block peals

I have found 17 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [29 to 45] of round blocks where the sixes can be rearranged to give 51 complete B-blocks. Here is a set of blocks which gives peals.

45 round blocks, signature: 50:21+90

2314567QS---------P--------P---P---------P--P--P-------P--P--------P---------PP*1(1)
7352614QS---------P--------P---P---------P--P--P-------P--P--------P---------PP*1(1)
4367152QS---------P--------P---P---------P--P--P-------P--P--------P---------PP*1(1)
1427536QS--------PPP--------PPP------P-*1(1)
6742135QS--------PPP--------PPP------P-*1(1)
5274631QS--------PPP--------PPP------P-*1(1)
1652437QS---------P------P--P*1(1)
4562137QS---------P------P--P*1(1)
1732456QS---------P------P--P*1(1)
6234715QS---------P------P--P*1(1)
2617534QS---------P------P--P*1(1)
5167234QS---------P------P--P*1(1)
6514732QS---------P------P--P*1(1)
7154632QS---------P------P--P*1(1)
5437261QS---------P------P--P*1(1)
4123657QS--------P--P------P-*1(1)
4125736QS--------P--P------P-*1(1)
7641235QS--------P--P------P-*1(1)
2573164QS--------P--P------P-*1(1)
7643512QS--------P--P------P-*1(1)
2576431QS--------P--P------P-*1(1)

This is a three-part based set of blocks. It does not give exact three-part peals.

• CompLib 82787 618 bobs irregular three-part
• CompLib 83002 618 bobs irregular three-part
• CompLib 91882 618 bobs three-part

50 complete B-block peals

I have found 23 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [27 to 35] of round blocks where the sixes can be rearranged to give 50 complete B-blocks. Here is a set of blocks which gives peals.

31 round blocks, signature: 60:7+105

2314567QS---------P--------P---------PP---------P--------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P--------P---------PP---------P--------P---------P-----P---------P-----P---------P----P---------P---P---------P----P-----PP---P---------PP---------P--------P---------PP---------P----P--------P---------PP---PP*1(1)
6513472QS---------P--------P----PP--P-----P--P-P---------P-------P------PP--------PP-P-P---------P-------P-P---P----PPP--------PP---P----P---P---PP*1(1)
6531427QS---------P--------PP-----P----P---PPP---PP*1(1)
5412637QS--------PP--------PP*1(1)
3546217QS--------PP--------PP*1(1)
6512743QS-------P---P-----PP-*1(1)
6142537QS-------P-P-------P-P*1(1)

• CompLib 92712 621 bobs

49 complete B-block peals

I have found 12 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [31 to 35] of round blocks where the sixes can be rearranged to give 49 complete B-blocks. Here is a set of blocks which gives peals.

33 round blocks, signature: 60:9+105

2314567QS---------P--------P---------PP---------P--------P----P----P---------P---P---------P----P---------P-----P---------P----P---------P---P-P-P---------P-------P-------P--------P---------PP---PP*1(1)
6725134QS---------P-----P---------P-----P---------P----P---------P---P---------P----P-----PP-P-P---------P-------P------P---------PP---------P--------P*1(1)
6513472QS---------P--------P----PP--P-----P--P-P---------P-------P------PP--------PP-P-P---------P-------P-P---P----P-----P----P---P---PP*1(1)
6531427QS---------P--------PP-----P----P---PPP---PP*1(1)
5412637QS--------PP--------PP*1(1)
3546217QS--------PP--------PP*1(1)
6512743QS-------P---P-----PP-*1(1)
6142537QS-------P-P-------P-P*1(1))
2456317QS-------P-P-------P-P*1(1))

• CompLib 78017 603 bobs

48 complete B-block peals

I have found 14 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [29 to 35] of round blocks where the sixes can be rearranged to give 48 complete B-blocks. Here is the set of blocks which gives peals.

35 round blocks, signature: 54:5+96

2314567QS---------P----P----P------P-P----P----P---P---------P----P----P--P-------P----P----P-----P*3(1)
2654137QS---------P----P---P---P---------P--P-P----P---------P----P-----PP----P*3(1)
2356147QS---------P------P--P*1(1)
7246513QS---------P------P--P*1(1)
3716452QS---------P------P--P*1(1)

These blocks are from a group of order 3.

8 examples of exact theee-parts with 636 bobs

• CompLib 88655 no 9 bob run
• CompLib 97657
• CompLib 88617
• CompLib 97660
• CompLib 97662
• CompLib 97663
• CompLib 97664
• CompLib 97666 By bobbing Q-sets the number of bobs can be increased up to 690 bobs.
• CompLib 97568 645 bobs
• CompLib 88618 690 bobs - one of 32 examples

Number of bobs	Number of peals
636	8
645	72
654	263
663	493
672	488
681	228
690	32
Total	1584

The 2017 exact three-part peals have between 603 and 639 bobs and all have at least one 9 bob run per part; these have between 636 and 690 bobs.

Also

• CompLib 97714 606 bobs - irregular three-part

42 complete B-block peals

I have found 2 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [31, 35] of round blocks where the sixes can be rearranged to give 42 complete B-blocks. Here are the sets of blocks together with some peals. Both sets of blocks are based on a group of order 3.

31 round blocks, signature: 57:4+120

2314567QS---------P----P---P---P---------P--P-P----P---PPP-P----P----P---P---------P----P----P--P-------P----P----P-----P----PP--------PP---P----P----P----PP----P----P-----PP----P*3(1)
2613547QS---------P------P--P*1(1)
7243156QS---------P------P--P*1(1)
6753412QS---------P------P--P*1(1)

• CompLib 91897 612 bobs, exact three-part
• CompLib 97816 621 bobs, exact three-part
• CompLib 91986 630 bobs, exact three-part
• CompLib 91898 657 bobs, exact three-part These exact three-part peals range from 612 to 666 bobs, compared to 636 to 690 for the 48 complete B-block exact three-parts shown earlier, or 603 to 639 for the exact three-part peals published in 2017.

Number of bobs	Number of peals
612	1
621	9
630	34
639	70
648	84
657	56
666	16
Total	270

35 round blocks, signature: 54:5+111

2314567QS---------P-----PPP--------PP-------P-----P---------P----P-------PP--------PPP---P--------P---------PP---------P---PP--------PP---P*3(1)
5126347QS-------PP--P-----P----P---PPP-*3(1)
1723546QS--------PP--------PP*1(1)
5163724QS--------PP--------PP*1(1)
7562143QS--------PP--------PP*1(1)

• CompLib 85926 570 bobs, irregular three-part
• CompLib 77482 576 bobs, three-part
• CompLib 77446 576 bobs, three-part

36 complete B-block peals

I have found at least 84 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [25] of round blocks where the sixes can be rearranged to give 36 complete B-blocks. Here are the sets of blocks together with some peals. Most of the peals have already been published as the exact three-part peals from 2017, see Three-part bobs-only peals of Stedman Triples in The Ringing World Issue 5565 p1264 22 December 2017.

There sets of blocks are based on a group of order 3. The blocks have not been normalised by rotation to better show the similarities.

25 round blocks, signature: 60:1+165

4637251QS----P-----P---------PP--------P-P----PP----PPP--------P-----P---------P-P----PP--PP----PP----PP--PP--------PP--PPPP--PP--PP--P--------P-----PP---P--------P-----P---------P-PPP--PP--PP----PP--PP--P----*3(1)

• CompLib 37420 Exact three-part Op. 1, 603 bobs
• CompLib 37428 Exact three-part Op. 496, 603 bobs

4637251QS----P-----P---------PP--------P-P----PP--PP----PP--PPPP--PP--PP--P--------P-----PP---P--------P-----P---------P-P----PP--PPPPP--------P-----P---------P-P----PP--PP----PP--------PP--PP----PP--PP--P----*3(1)

• CompLib 37421 Exact three-part Op. 10, 603 bobs
• CompLib 37427 Exact three-part Op. 487, 603 bobs

4637251QS----P-----P---------P-P----PP----PPP--------P-----P---------P-PPP--PP--------PP----PP--PP--PP----PP--PP--P--------P-----P---------PP--------P-P----PP--PP----PP--PPPP--PP--PP--P--------P-----PP---P----*3(1)

• CompLib 37422 Exact three-part Op. 55, 603 bobs

4637251QS----P-----P---------P-PPP--PP--------PP--PP--P--------P-----P---------PP--------P-PPP--PP----PPP--------P-----P---------P-PPP--PP--------PP----PP--PP--------PP--PPPP--PP--PP--P--------P-----PP---P----*3(1)

• CompLib 37425 Exact three-part Op. 82, 603 bobs
• CompLib 37430 Exact three-part Op. 568, 603 bobs

4637251QS----P-----P---------P-P----PP--PP----PP--------PP--PPPPP--------P-----P---------P-P----PP--PP----PP--PP--P--------P-----P---------PP--------P-P----PP--PP----PP--PPPP--PP--PP--P--------P-----PP---P----*3(1)

• CompLib 36006 Exact three-part Op. 109, 603 bobs
• CompLib 36034 Exact three-part Op. 109 Queen’s rotation, 603 bobs
• CompLib 77814 Exact three-part Op. 284, 639 bobs
• CompLib 37431 Exact three-part Op. 595, 603 bobs
• CompLib 37432 Exact three-part Op. 622, 603 bobs

4637251QS----P-----P---------P-PPP--PP--------PP--PP--P--------P-----P---------PP--------P-PPP--PP--PP----PP--------PP--PPPPP--------P-----P---------P-P----PP--------PP--PPPP--PP--PP--P--------P-----PP---P----*3(1)

• CompLib 37426 Exact three-part Op. 136, 603 bobs
• CompLib 37429 Exact three-part Op. 541, 603 bobs

A summary of all those exact three-parts with 36 complete B-blocks:

Number of bobs	Number of peals
603	12
612	96
621	288
630	384
639	192
Total	972

These are some irregular blocks, but based on the blocks above.

25 round blocks, signature: 60:1+159

3467251QS-------PP----P-P---------P-----P--------P--PP--PP----PP--PP----P-P---------P-----P--------PPP----PP----P-P---------P-----P--------P--PP--PP----PP--PP--PPP-P---------P-----P--------P--PP--PP----PP--PP--PPP-P---------P-----P--------P--PP--PP----PP--PP----P-P---------P-----P--------P--PP--PP----PP--PP----P-P---------P-----P--------P--PP--PP--------PP----P-P--------PP---------P-----P--------P--PP--PP----PP--PP----P-P---------P-----P--------P--PP--PP----PP--PP--PPP-P---------P-----P--------P---PP-----P--------P--PP--PP--PPPP--PP--------PP--PP----PP----PP--PP----P-P---------P-----P--------P--PP--PP-*1(1)

• CompLib 77588 609 bobs, very irregular theee-part

4637251QS----P-----P---------P-P----PP--------PP--PP--P--------P-----P---------P-P----PP--PP----PP--PP--P--------P-----P---------PP--------P-P----PP--PP----PP--PPPP--PP--PP--P--------P-----PP---P--------P-----P---------P-P----PP--PP----PP--PP--P--------P-----P---------P-PPP--PP--PP----PP--PP--P--------P-----P---------P-PPP--PP--PP----PP--PP--P--------P-----P---------P-P----PP--------PP--PP--P--------P-----P---------P-P----PP--------PP--PP--P--------P-----P---------P-P----PP--PP----PP----PP--PP--PP----PP--PP--P--------P-----P---------P-P----PP--PP----PP--PP--P--------P-----P---------P-PPP--PP----PPP----*1(1)

• CompLib 77964 645 bobs, irregular

25 round blocks, signature: 60:1+171

4637251QS----P-----PP---P--------P-----PP---P--------P-----P---------PP--------P-PPP--PP--PPPPP--------P-----P---------P-P----PP--PP----PP--PP--P--------P-----P---------PP--------P-P----PP--PPPPP--------P-----P---------PP--------P-P----PP--PPPPP--------P-----P---------PP--------P-P----PP--PP----PP--PPPP--PP--------PP--PP----PP----PP------PPPP--PP--PP--P--------P-----PP---P--------P-----P---------PP--------P-P----PP--PP----PP--PPPP------PP----PP--PPPP--PP--PPPP--PP---PP---PP--------PP---PP---PP--PP----PP--------PP--PPPPP--------P-----PP---P--------P-----PP---P--------P-----P---------P-P----PP----PPP----*1(1)

• CompLib 97879 597 bobs

24 complete B-block peals

I have found 272 sets of round blocks which together with some B-blocks exactly cover the extent in an odd number [23 to 33] of round blocks where the sixes can be rearranged to give 24 complete B-blocks. Here are examples of two sets of blocks which give peals.

23 round blocks, signature: 66:5+171

2314567QS---------P--------P---P-------PP--------PPP---P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P---P-------PPP---P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P----PP--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P---P-------PPP---P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P---P-------PPP---P----PP--------PPP--P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P---P-------PPP---P----PP--------P--P--------PP---PP*1(1)
6451327QS--------PP---PP--------PP---PP*1(1)
2314675QS-----P--P------P--P-*1(1)
2341765QS-----P--P------P--P-*1(1)
6315274QS-----P--P------P--P-*1(1)

• CompLib 76542 597 bobs

27 round blocks, signature: 56:9+165

2314567QS---------P--------P---P-------PP--------PPP---P----PP--------PPP--P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P----PP--------PP---PP*1(1)
7345126QS---------P--------P---P-------PP--------PPP---P----PP--------PPP--P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P----PP--------PP---PP*1(1)
6351472QS---------P--------P---P-------PP--------PPP---P----PP--------PPP--P----PP--------P--P--------PP---PP---------PPPPP--------PP---PP--------PP-PP------P----PP--------PP---PP*1(1)
6451327QS--------PP---PP--------PP---PP*1(1)
2514376QS--------PP---PP--------PP---PP*1(1)
7145362QS--------PP---PP--------PP---PP*1(1)
2314675QS-----P--P------P--P-*1(1)
2341765QS-----P--P------P--P-*1(1)
6315274QS-----P--P------P--P-*1(1)

• CompLib 60827 606 bobs, three-part peal
• CompLib 37975 606 bobs, three-part peal
• CompLib 37408 606 bobs, three-part peal
• CompLib 38015 609 bobs, three-part peal
• CompLib 38016 609 bobs, three-part peal

12 complete B-block peals

These are the 10-part peals of 1995 and 2012 based on group [5.04]. See Bobs-only Stedman Triples made easy, The Ringing World, 11 August 1995, p841, Ringing Theory June 2012 Ringing Theory July 2012 and ‘Stedman Triples and Similar Fascinations’ for the 152 peals. There is nothing new here.

1995 compositions

Set @1, 7 round blocks, signature: 82:5+390

2314567QSPP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP--P----PP-PP-P--P-*2(1)
3425167QSPP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP--P----PP-PP-P--P-*2(1)
4531267QSPP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP--P----PP-PP-P--P-*2(1)
5142367QSPP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP--P----PP-PP-P--P-*2(1)
1253467QSPP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP--P----PP-PP-P--P-*2(1)

Peals of 438 to 441 bobs

• CompLib 28944 438 bobs, Cholsey version
• CompLib 28946 438 bobs, OLEM version
• CompLib 28945 441 bobs, original version
• CompLib 28947 441 bobs, Aston Martin version
• CompLib 48969 438 bobs, reversed

These are based on a bobs-only block from group [5.04], linking in pairs, excluding sixes with 76 behind which then link as B-blocks.

2012 compositions

Set @3, 5 round blocks, signature: 82:3+378

2314567QS-----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP---P--P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP---P--P--PP--P-PPPP--PP---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PP*2(1)
2354176QS-----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PP*2(1)
6243517QS---P-P--PP--P-PPPP--PP*2(1)

Peals of 441 to 456 bobs

• CompLib 102723 441 bobs

Set @2, 5 round blocks, signature: 82:3+384

2314567QS---P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P--P---PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P--PPP-PP-P--P-PP-*2(1)
4527613QS----PP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P-P---PP--PPPP-P--PP--P--PPP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P--PPP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP-*1(1)
6527431QS----PP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P-P---PP--PPPP-P--PP--P--PPP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P--PPP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP-*1(1)

Peals of 438 to 450 bobs

• CompLib 31021 438 bobs, exact two-part

Set @4, 7 round blocks, signature: 82:5+378

2314567QS-----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PP*2(1)
5213647QS---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP---P--P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP*1(1)
6243517QS---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP---P--P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP*1(1)
1243576QS-------PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-*1(1)
4213675QS-------PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-*1(1)

Peals of 444 to 453 bobs

• CompLib 102732 444 bobs

Set @5, 9 round blocks, signature: 82:7+372

2314567QS-----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP---P--P--PP--P-PPPP--PP---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PP*1(1)
2316745QS-----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PPP--P--PP--P-PPPP--PP---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP---P--P--PP--P-PPPP--PP---P-P--PP--P-PPPP--PP--P----PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-PP*1(1)
6213457QS-------PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-*1(1)
1243576QS-------PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-*1(1)
4213675QS-------PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-*1(1)
1263754QS-------PP-PP-P--P-PP---PPP--P-P----PPPP--P--P----PP-P--P-PP-*1(1)
6243517QS---P-P--PP--P-PPPP--PP*2(1)

Peals of 444 to 453 bobs

• CompLib 37682 444 bobs, exact two-part
• CompLib 37713 444 bobs, exact two-part

Set @6, 9 round blocks, signature: 82:7+372

2314567QS---P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P--P---PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP----P--PP--PPPP-P--PP--P-P---PP--PPPP-P--PP--P--P---PP-P--P-PP-*2(1)
1327456QS----PP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP-*2(1)
4327165QS----PP-PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP-*2(1)
1627543QS-------PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP-*1(1)
4527613QS-------PP-P--P-PP----P--P--PPPP----P-P--PPP---PP-P--P-PP-PP-*1(1)
1475236QS--P-P---PP--PPPP-P--PP*2(1)
4176235QS--P-P---PP--PPPP-P--PP*2(1)

Peals of 447 to 456 bobs

• CompLib 37714 456 bobs, exact two-part

Summary

These are the results of ad-hoc searches, and are not comprehensive. A lot of them were obtained by taking an existing peal I had found, keeping some parts fixed and varying other parts.

For example, sometimes I took one peal, bobbed all the Q-sets to get an odd number of round blocks, and kept the paired B-blocks as fixed because paired B-blocks are useful as there are a 6 ways each pair can be expressed, which helps linking everything together, and also if they were variable a search could come up with any of those 6 forms which wouldn’t be significantly different, but would just flood the results.

I then took the remaining sixes and searched to see how many sets of round blocks I could obtain. I might also impose other limits like the total number of bobs (because otherwise the search might just turn up 84 B-blocks), and number of complete B-blocks, and also that any Q-sets should be bobbed (to restrict equivalent solutions). My searches couldn’t easily filter results of odd numbers of round blocks vs even numbers so I had to do that once I had say 1000 results. If I got less than 1000 when the search terminated then I knew I had found all the blocks subject to the conditions. I could then try to link the blocks into a peal, but there would be a free choice of 6 for each of the paired B-blocks. Sometimes if I wanted to reduce the number of bobs I would choose the instances of the paired B-blocks to maximise the number of available Q-sets and then try to link the blocks without changing the types of the B-blocks. I could also try other restrictions such as not allowing 7 bobs in a row, and finding 8 plains in a row.

The number of bobs now ranges from 438 to 456 (existing 10-part peals, including some exact two-parts) and 528 to 711 (one-part peals). The exact three-part peals now range from 603 to 690 bobs. With 84 B-blocks there are 840 bobs, so 123 omits on Q-sets could link those to 2 blocks with 717 blocks. An upper limit on the number of bobs therefore seems to be 714, but that would require a 2 blocks to 1 link with 3 omits, or a 4 blocks to 1 with 6 omits etc. which seems unlikely, so perhaps 711 bobs is the limit.

The 528 bob peal CompLib 86761 has 4 Q-sets which could not be plained without splitting it back into multiple blocks, and there was another peal CompLib 92761 where if all the Q-sets were plained there would be 501 bobs (but multiple blocks), so perhaps a one-part peal using B-blocks can be found with fewer than 528 bobs but I am guessing to achieve fewer than 500 bobs would be hard.

This graph shows the minimum number of bobs found so far in a peal and a possible maximum number of bobs against the number of complete B-blocks.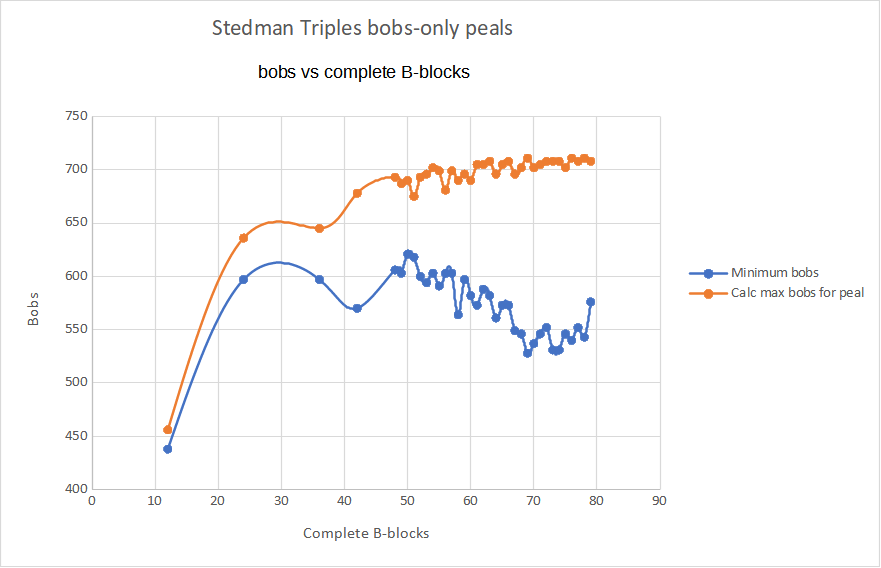

I found several peals with 8 plains in a row but they can’t be arranged to put all at the start or all at the end of a peal with a normal start; it needs to start or end with a bob, so at best with my peals you can end with 8 plains and a bob, or 7 plains. Perhaps this can be improved on.

CompLib 84174 is interesting as all the bobs come in multiples of 2 (2,4 or 6) except for 18 single bobs, but it is a one-part. The treble does 0,2 or 6 bobs behind. Compare with the exact 3-part from 2017 CompLib 36006, which has 9 runs of 1 bob, 3 runs of 3 bobs and 15 runs of 5 bobs and the 7 does either 2 or 6 bobs behind.

Among the things that didn’t work for me:

7-part peals

7-part peals - group [7.07]

There is no bobs-only exact 7-part. There are multiple sets of blocks with a 7-part group with an odd number [5,21,35] of round blocks, but it doesn’t seem possible to link them with bobs or omits. Here are some peals with singles to link the blocks

35 round blocks, 49 complete B-blocks, signature 63:14+105

3124567QS-----PPP--------PP----P---P---------P--------P---------PP---------P---*1(7)
4125367SQ-------P--P------P--*1(7)
4236175SQ----------*1(7)
5316472SQ----------*1(7)
1627354SQ----------*1(7)

• CompLib 48931 651 bobs, 42 singles

5 round blocks, 14 complete B-blocks, signature 84:5+252

3124567QS-----P-------PP-P-----PP--PP---------P--PP-----P-PPP----PP-PP-P-P-P-----P---*7(1)
6421375QS--PP----PP---P---P--------PP*7(1)
4125367SQ-----P*7(1)
1536472QSP-----*7(1)
7165324QSP-PP*7(1)

• CompLib 48932 560 bobs, 56 singles

35 round blocks, 49 complete B-blocks, signature 56:7+105

1234567QS--P--P--------P---------PP-------PP-P---------P--P---PPP--------P---------P-----*1(7)
4267351SQ----------*1(7)
1637452QS----------*1(7)
5316472SQ----------*1(7)
3617254SQ----------*1(7)

• CompLib 48954 651 bobs, 42 singles

6-part peals

6-part peals - group [6.32]

There can’t be an exact 6-part bobs-only peal, but the group could generate blocks which link in pairs to give 3 round blocks. When I was working with Dr Michael Haythorpe he ran my program in 2013 and we found the following sets of an odd number of blocks, shown in file odd.txt. Unfortunately I cannot see a way of linking the blocks with just bobs. That’s an especial pity because the set giving 5 round blocks has only 402 bobs.

We also found some single blocks, shown in file single.txt, which when expanded for a peal formed 2 or 6 round blocks (but unfortunately not 3). This shows that the 6-part graph is Hamiltonian. Example peals using singles are here:

• CompLib 49158 540 bobs, 6 singles
• CompLib 49177 540 bobs, 6 singles

5-part peals

5-part peals - group [5.05]

As already published, there just one instance (+rotations/reversal) of a single block (actually from the 10-part group, so made of two identical sections), but it links to itself and cannot be linked by Q-sets of bobs or omits.

• CompLib 28949 450 bobs, 10 singles

There are sets of multiple blocks with odd numbers of blocks when expanded to all the rows (e.g. the original 10-part peals) which can be linked with Q-sets of bobs or omits to provide the existing 10-part peals.

The magic blocks appear in a 5-part search, together with the remaining B-blocks, but cannot be linked without changing the type of some of the B-blocks, so there isn’t a 5-part based magic block peal. There might be other sets of an odd number of blocks - I haven’t found them yet.

4-part peals

4-part peals - group [6.26]

Not much success here - but the search space gets larger as the groups get smaller. The graph is Hamiltonian, but the example I found, from a 20-part search) divides into 4 1-part blocks. This doesn’t stop there being an exact 4-part out there.

3124567QSP--PP--P---------P--PPP---------P--P--P--P*5(4)

Generators [1543267, 1425376] group order 4

3124567QSP---P---------P--P--P---P--P---------P--PPP---------P--P-----PP--P---------P-----P--P---P---------P--P--P---P--P---------P--PPP---------P--P-----PP--P---------P-----P---PP---------P--P-----PP--P---------P-----P*1(1)

• CompLib 104651 660 bobs, 4 special calls

4-part peals - group [4.04]

Not directly useful for a bobs-only peal. This is the only group for Stedman Triples where I don’t know whether the reduced graph is Hamiltonian i.e. can a search just turn up one block

4-part peals - group [6.35]

Not directly useful for a bobs-only peal. Is a Hamiltonian graph (i.e. search can find one block), but then need 4 of those blocks cover all the sixes.

4-part peals - group [4.05m]

An in course subgroup of the Thurstans’ 20-part out of course group. Not directly useful for a bobs-only peal. Is a Hamiltonian graph.

4-part peals - group [4.06m]

Two pairs swapping independently Not directly useful for a bobs-only peal. Is Hamiltonian though, giving this nice peal with singles just swapping 12 or 34 in the parts:

2314567QSP--P-PPP--P-PP-P-P-P-PP--P--P--P---P--P--PP--PP--PP------P--P-PP-P-PPP-P------P-PP------PP-P--PPPPP-P--P-----P--P-P-PP-P--P---P-P--P-P---P--P-P--PP-PPP--------PPP----P-PPP-P-PP---PPP-P----PPP---P--PP---PP------*1(1)

• CompLib 66787 486 bobs, 6 singles

3-part peals

3-part peals - group [6.33]

Lots of peals - but too big to search completely. I think I did complete a search choosing 4 pairs of complementary B-blocks and one block with the remaining sixes (200 sixes), anyway it was how I found the 42 and 48 complete B-block exact 3-parts.

2-part peals

2-part peals - group [4.07]

Nothing new after the 2012 peals.

2-part peals - group [2.01]

One pair swapping. Not directly useful for a bobs-only peal. Is Hamiltonian though, and gives a peal which looks like Slack’s two-part, but comes round half-way if you replace the single with a bob.

• CompLib 66793 508 bobs, 2 singles

Slack’s peal is actually made of 4 blocks and does not come round if you replace the single with a bob or a plain and has more bobs (596 vs 508), so mine is cleaner, but not of the same historical interest.

• CompLib 29011 596 bobs, 2 singles. G W Slack

Favourites

• CompLib 46069 708 bobs, isolated omits where there are just 8 omits after quick sixes
• CompLib 93429 711 bobs, only 8 omits after a quick six
• CompLib 60810 711 bobs with one double omit
• CompLib 84174
  • 594 bobs
  • 18 isolated bobs
  • 121 runs of 2 bobs
  • 7 runs of 4 bobs
  • 51 runs of 6 bobs
• CompLib 82483 591 bobs, only 13 runs with an odd number of bobs
• CompLib 86761 528 bobs
• CompLib 88655 exact three-part, 636 bobs, no 9 bob run
• CompLib 88618 exact three-part, 690 bobs
• CompLib 91897 612 bobs, exact three-part
• CompLib 36006 exact three-part Op. 109, 603 bobs
• CompLib 28944 438 bobs, Cholsey version
• CompLib 31021 438 bobs, exact two-part

Conclusion

These are the last of the bobs-only peals for now; I have some unpublished peals but they are not significantly different from the published ones. The collection is here: CompLib ‘Stedman Triples bobs-only peals’.

Table of Contents

• Bobs-only extents of Stedman Triples
  • Introduction
  • Magic Block Peals
  • Other 79 complete B-block peals
    • 79 round blocks
      • Signature: 10:5+15
      • Signature: 10:5+15
      • Signature: 10:5+15
  • 78 complete B-block peals
    • 73 round blocks
      • Signature: 12:1+21
    • 75 round blocks
      • Signature: 12:3+21
    • 77 round blocks (a)
      • Signature: 11:4+18
    • 77 round blocks (b)
      • Signature: 11:4+18
  • 77 complete B-block peals
    • 73 round blocks (a)
      • Signature: 13:2+21
    • 73 round blocks (b)
      • Signature: 13:2+21
    • 75 round blocks (a)
      • Signature: 13:4+21
      • Signature: 13:4+21
    • 75 round blocks
      • Signature: 14:5+21
    • 75 round blocks (b)
      • Signature: 14:5+21
    • 75 round blocks (c)
      • Signature: 14:5+21
    • 75 round blocks
      • Signature: 14:5+21
  • 76 complete B-block peals
    • 71 round blocks (a)
      • Signature: 18:5+33
    • 71 round blocks (b)
      • Signature: 14:1+24
    • 71 round blocks (c)
      • Signature: 19:6+33
    • 71 round blocks (d)
      • Signature: 19:6+33
    • 71 round blocks (e)
      • Signature: 19:6+33
    • 71 round blocks (f)
      • Signature: 19:6+33
    • 71 round blocks (g)
      • Signature: 19:6+33
    • 71 round blocks (h)
      • Signature: 19:6+33
    • 73 round blocks (a)
      • Signature: 18:7+33
    • 73 round blocks (b)
      • Signature: 18:7+33
    • 75 round blocks (a)
      • Signature: 14:5+21
    • 75 round blocks (b)
      • Signature: 14:5+21
  • 75 complete B-block peals
    • 71 round blocks
      • Signature: 15:2+27
      • Signature: 19:6+33
  • 74 complete B-block peals
    • 67 round blocks, signature: 20:3+33
    • 67 round blocks, signature: 22:5+45
    • 67 round blocks, signature: 21:6+45
    • 69 round blocks, signature: 20:5+33
    • 69 round blocks, signature: 18:3+33
    • 69 round blocks, signature: 20:5+33
    • 69 round blocks, signature: 21:6+33
    • 69 round blocks, signature: 20:5+33
    • 71 round blocks, signature: 20:7+33
    • 73 round blocks, signature: 20:9+33
    • 73 round blocks, signature: 21:10+33
    • 73 round blocks, signature: 20:9+33
    • 73 round blocks, signature: 21:10+33
  • 73 complete B-block peals
    • 67 round blocks
      • Signature: 21:4+33
    • 69 round blocks
      • Signature: 21:6+33
    • 71 round blocks
      • Signature: 21:8+33
  • 72 complete B-block peals
    • 67 round blocks, signature: 24:7+45 (a)
    • 67 round blocks, signature: 24:7+45 (b)
    • 67 round blocks, signature: 22:5+39
    • 67 round blocks, signature: 22:5+33
    • 69 round blocks, signature: 23:8+39 (a)
    • 69 round blocks, signature: 23:8+39 (b)
    • 69 round blocks, signature: 23:8+39 (c)
    • 71 round blocks, signature: 24:11+39
  • 71 complete B-block peals
    • 63 round blocks, signature: 25:4+42
    • 65 round blocks, signature: 23:4+39
    • 67 round blocks, signature: 25:6+39
    • 67 round blocks, signature: 24:7+45
    • 67 round blocks, signature: 23:6+51
    • 67 round blocks, signature: 25:8+45
    • 67 round blocks, signature: 23:6+39
    • 67 round blocks, signature: 24:7+45
    • 69 round blocks, signature: 24:9+39
    • 69 round blocks, signature: 23:8+39
  • 70 complete B-block peals
    • 63 round blocks, signature: 28:7+45
    • 63 round blocks, signature: 26:5+45
    • 67 round blocks, signature: 28:11+45
    • 67 round blocks, signature 24:7+45
  • 69 complete B-block peals
    • 57 round blocks (a), signature: 29:2+45
    • 57 round blocks (b), signature: 29:2+45
    • 59 round blocks, signature: 28:3+45
    • 61 round blocks, signature: 27:4+45
    • 63 round blocks, signature: 26:5+45
    • 65 round blocks, signature: 25:6+45
    • 67 round blocks, signature: 29:12+45
  • 68 complete B-block peals
    • 55 round blocks, signature: 32:3+57
    • 65 round blocks, signature: 28:9+51
    • 71 round blocks, signature: 24:11+45
  • 67 complete B-block peals
    • 63 round blocks, signature: 30:9+51
    • 67 round blocks, signature: 28:11+45
  • 66 complete B-block peals
    • 47 round blocks, signature: 39:2+63
    • 51 round blocks, signature: 36:3+57
    • 63 round blocks, signature: 32:7+51
    • Three-part peals
      • Exact three-parts: all the parts are called the same.
      • Other three-parts:
        • Irregular three-parts
  • 65 complete B-block peals
    • 53 round blocks, signature: 35:4+57
    • 61 round blocks, signature: 35:14+63
  • 64 complete B-block peals
    • 51 round blocks, signature: 38:5+69
    • 51 round blocks, signature: 38:5+63
    • 61 round blocks, signature: 31:8+57
    • 63 round blocks, signature: 28:7+54
  • 63 complete B-block peals
    • 47 round blocks, signature: 39:2+63
    • 47 round blocks, signature: 39:2+63
  • 62 complete B-block peals
    • 45 round blocks, signature: 42:3+69
    • 49 round blocks, signature: 42:7+69
    • 57 round blocks, signature: 40:13+66
    • 59 round blocks, signature: 32:7+59
    • 59 round blocks, signature: 40:15+66
    • 63 round blocks, signature: 28:7+57
    • 69 round blocks, signature: 28:13+57
  • 61 complete B-block peals
    • 43 round blocks, signature: 45:4+72
    • 45 round blocks, signature: 43:4+69
    • 45 round blocks, signature: 43:4+69
    • 49 round blocks, signature: 43:8+93
  • 60 complete B-block peals
    • 47 round blocks, signature: 46:9+81
    • 47 round blocks, signature: 46:9+81
    • 59 round blocks, signature: 43:18+75
  • 59 complete B-block peals
    • 47 round blocks, signature: 44:7+75
  • 58 complete B-block peals
    • 45 round blocks, signature: 50:11+99
    • 63 round blocks, signature: 28:7+57
  • 57 complete B-block peals
    • 41 round blocks, signature: 49:6+81
    • 55 round blocks, signature: 47:18+81
  • 56 complete B-block peals
    • 55 round blocks, signature: 42:13+81
    • 61 round blocks, signature: 32:9+69
  • 55 complete B-block peals
    • 37 round blocks, signature: 52:5+87
    • 47 round blocks, signature: 44:7+87
  • 54 complete B-block peals
    • 35 round blocks, signature: 56:7+93
    • 35 round blocks, signature: 54:5+90
    • 39 round blocks, signature: 54:9+105
    • 45 round blocks, signature: 54:15+90
  • 53 complete B-block peals
    • 35 round blocks, signature: 56:7+93
  • 52 complete B-block peals
    • 33 round blocks, signature: 57:6+99
  • 51 complete B-block peals
    • 45 round blocks, signature: 50:21+90
  • 50 complete B-block peals
    • 31 round blocks, signature: 60:7+105
  • 49 complete B-block peals
    • 33 round blocks, signature: 60:9+105
  • 48 complete B-block peals
    • 35 round blocks, signature: 54:5+96
  • 42 complete B-block peals
    • 31 round blocks, signature: 57:4+120
    • 35 round blocks, signature: 54:5+111
  • 36 complete B-block peals
    • 25 round blocks, signature: 60:1+165
    • 25 round blocks, signature: 60:1+159
    • 25 round blocks, signature: 60:1+171
  • 24 complete B-block peals
    • 23 round blocks, signature: 66:5+171
    • 27 round blocks, signature: 56:9+165
  • 12 complete B-block peals
    • 1995 compositions
    • Set @1, 7 round blocks, signature: 82:5+390
    • 2012 compositions
    • Set @3, 5 round blocks, signature: 82:3+378
    • Set @2, 5 round blocks, signature: 82:3+384
    • Set @4, 7 round blocks, signature: 82:5+378
    • Set @5, 9 round blocks, signature: 82:7+372
    • Set @6, 9 round blocks, signature: 82:7+372
• Summary
  • 7-part peals
    • 7-part peals - group [7.07]
    • 35 round blocks, 49 complete B-blocks, signature 63:14+105
    • 5 round blocks, 14 complete B-blocks, signature 84:5+252
    • 35 round blocks, 49 complete B-blocks, signature 56:7+105
  • 6-part peals
    • 6-part peals - group [6.32]
  • 5-part peals
    • 5-part peals - group [5.05]
  • 4-part peals
    • 4-part peals - group [6.26]
    • 4-part peals - group [4.04]
    • 4-part peals - group [6.35]
    • 4-part peals - group [4.05m]
    • 4-part peals - group [4.06m]
  • 3-part peals
    • 3-part peals - group [6.33]
  • 2-part peals
    • 2-part peals - group [4.07]
    • 2-part peals - group [2.01]
• Favourites
• Conclusion
• Table of Contents